H30 嵯峨野高校 京都こすもす科 数学
嵯峨野高校京都こすもす科の数学問題の詳解です。
概説
今年度の京都府立嵯峨野高等学校 京都こすもす科の数学の入試問題解説です。 今年の問題で必ず得点しなければならないのは,大問1 (1),(2),(4),(5),大問2 (1),(2),大問4(1),大問5 (1)です。
最も難しく正答率が低かったと予想されるのは大問3です。この問題は捨てても大丈夫ですが、詳しく解説しました。また,大問1 (3)も正答率が低かったと思われます。三平方の定理を用いて方程式を立てる解法が分からなければ正解するのは難しいです。大問6
(1)は,比較的簡単で手計算で数えても解答できますが,(2)は考え方を記述させる問題になっています。これが曲者で,与えられた条件を真正直に使おうとすると解答できません。(3)は,(2)が出来れば解答できます。
嵯峨野高校京都こすもす科の数学の問題は,解答に必要な計算の道具立てこそ中学数学の範囲ですが,高得点を取るためには,高校の数学Ⅰ,数学Aの知識を用いて考える必要があり,数学Ⅰ・Aの基本問題を学習しておく必要があります。例えば今年度の問題では,大問1の(3)で平方完成,大問5の(2)で一
般の二次関数の知識が必要になります。また,大問6の(1)は,整数に関する知識があれば解きやすいです。また,(2)には高校レベルの分母の有理化の計算技法が必要です。
最後に,合格するためには確実に得点する問題と捨てるべき問題を見極めなければなりません。しかし,普段の勉強では捨て問にすべき難問に取り組んでください。難問が難問である所以がが理解できていて、初めて実戦での見極めが可能になります。
大問1
小問(1)は準備体操です。
小問(2)は2乗の差が和と差の積になることを思い出して下さい。
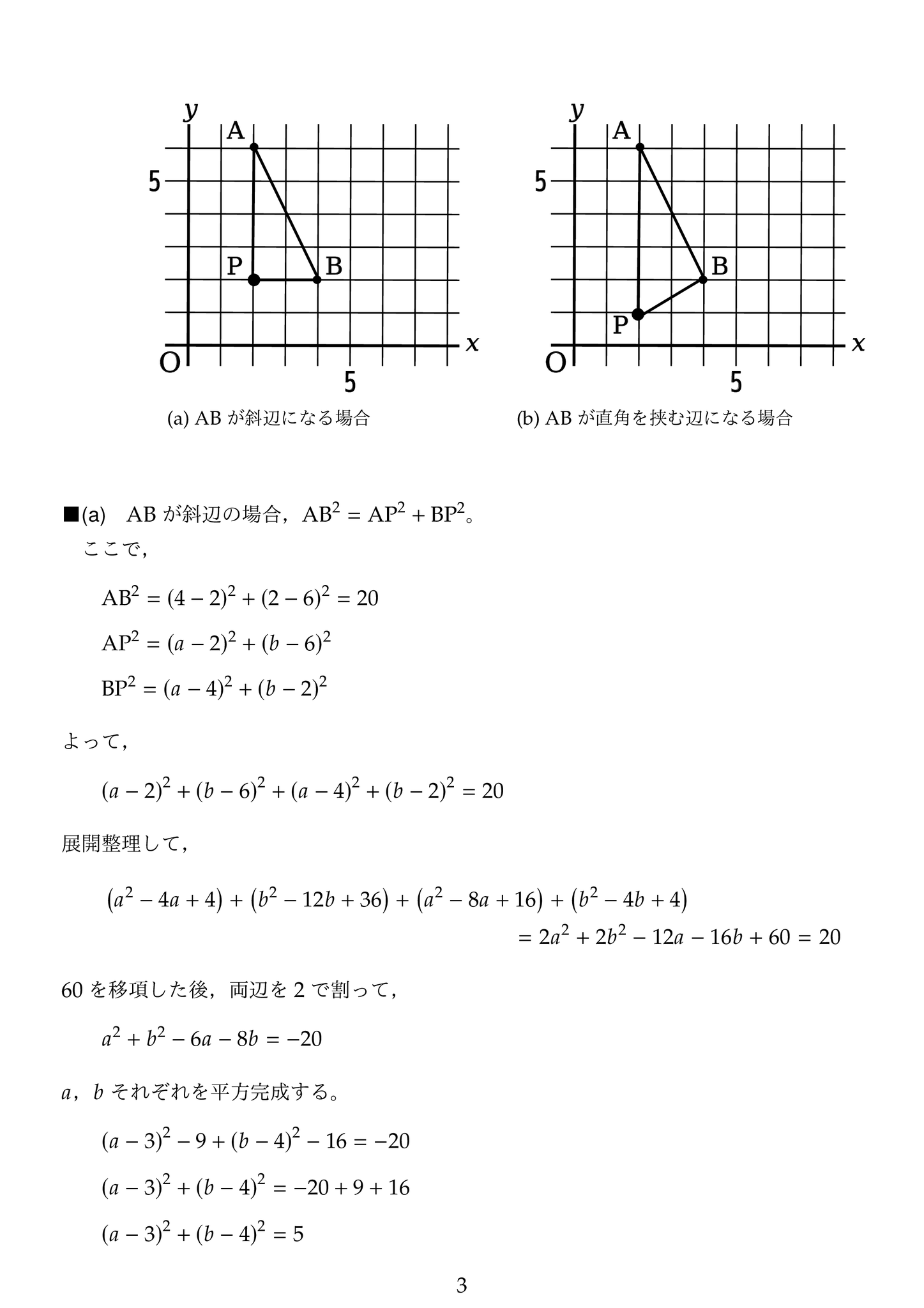
小問(3)は正解率が低かったと思います。2つのサイコロの目の組み合わせを全て確認していたのでは時間がかかり過ぎます。三平方の定理を用いて方程式を使って解かなければ正解できないです。この解答法を考えられなければ捨てて下さい。また,途中の計算で高校の数学Ⅰで扱う平方完成の計算技法が必要
となります。
小問(4)は直角三角形の相似の問題です。相似比と面積比を間違いなく計算できれば正解できます。
小問(5)は円周角の定理の問題です。時計の長針と短針の進む速さから,中心角の時間変化の式を立てて下さい。なお,解答では省略しましたが,求めた秒数において秒針が長針と短針の間にあると円周角の定理が使えなくなります。この設問では秒針が,長針と短針の間にはありませんので円周角の定理が成り
立っています。
大問2
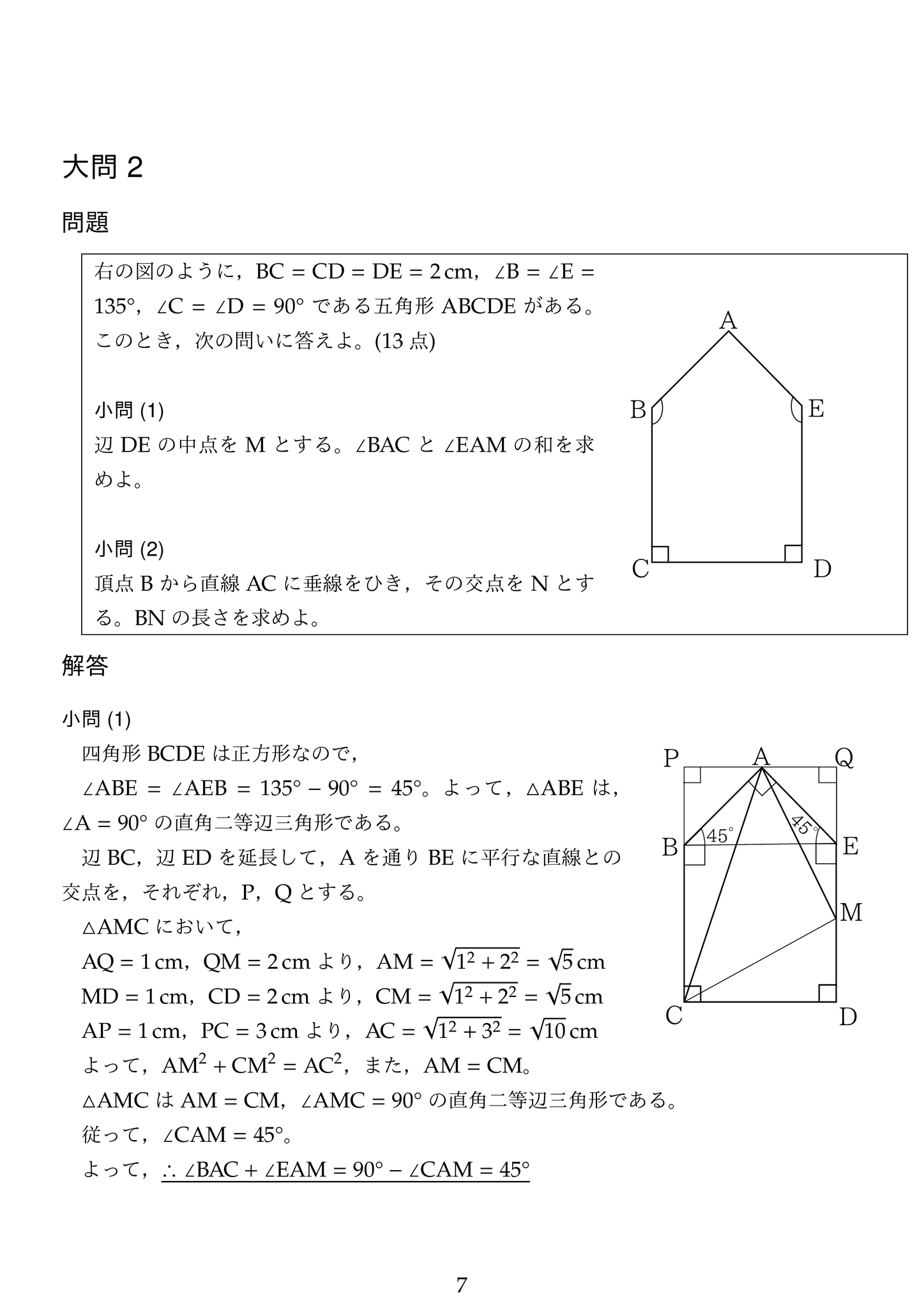
この問題は合格のための必須問題です。
直角三角形が使えるので,三平方の定理を使って辺の長さを計算して考えます。
(1) △ABEが直角二等辺三角形なので,角BAE=90°です。AM,AC,CMの長さを三平方の定理で計算して,△AMCが直角二等辺三角形である事に気づいて下さい。この問題のように直角三角形が使える時は三平方の定理で辺の長さを求めて考えることが解法の定石です。
(2) 垂線の長さを求める問題は,面積を使って考えるのが解法の定石です。
△ABCの面積が,BCを底辺,APを高さとして求めることに気がつければOKです。
大問3
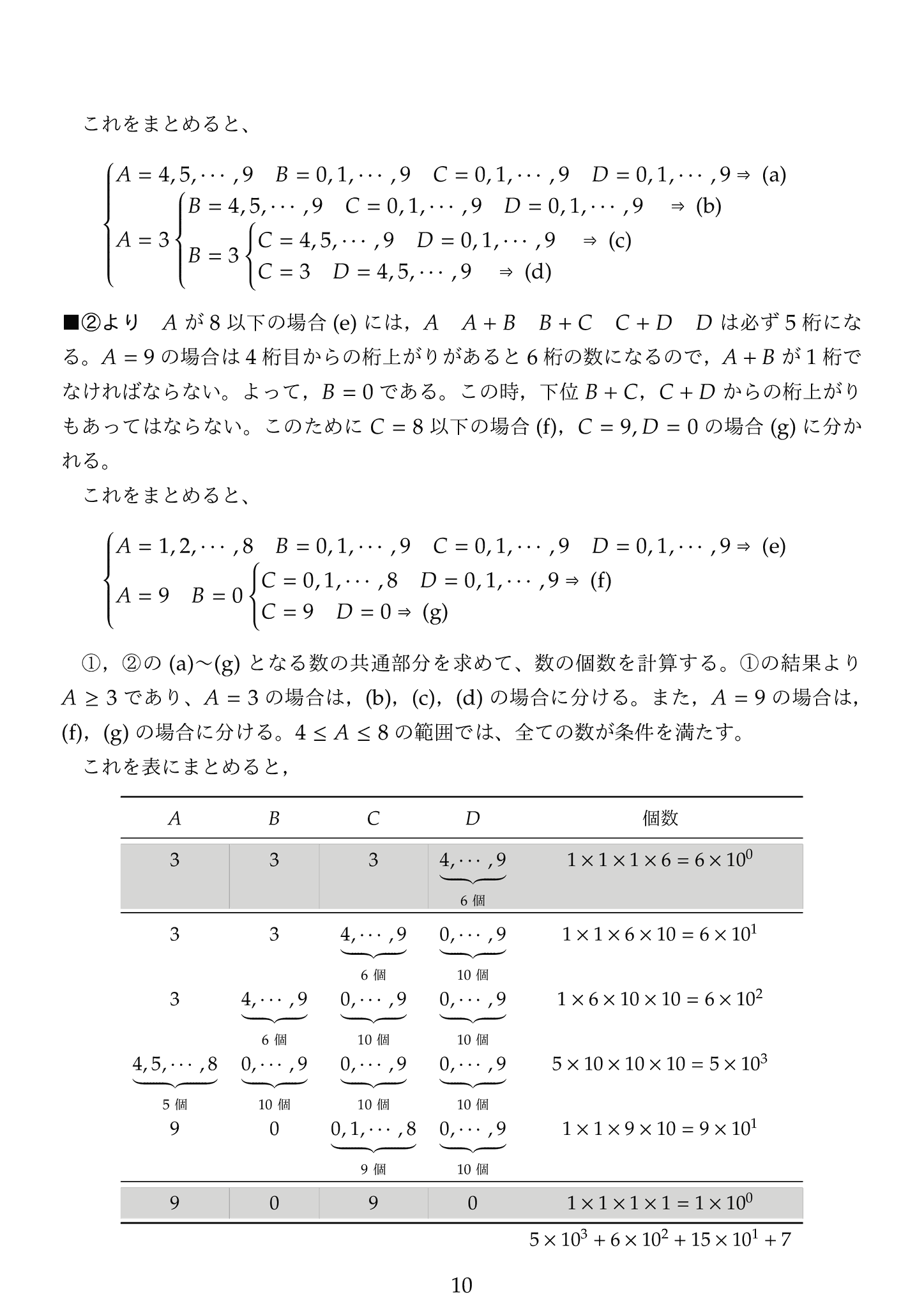
今年の数学の入試問題の最難問です。掛け算の筆算の仕組み,特に桁上がりが理解できているか,それに加えて場合の数の算が正確に出来るかを問う問題です。
解答に示したように相当量の計算が必要になります。正直なところ,私も正解に至るまでかなりの時間がかかりました。解答では n=5,6 についてのみ示していますが,(2)を解くために実際には n=2,3,4 も計算して初めて n が偶数と奇数の場合の f(n) が決まるメカニズムが理解できました。
入試的には捨て問ですが,如何に捨て問であるかを解答を見てじっくり味わって下さい。
大問4
(1) 三角錐ACFH は辺の長さが全て等しいので正四面体であること,そして,残された4つの三角錐が合同であることに気がついて下さい。1つの三角錐の体積は元の立方体の辺の長さから簡単に求まるので,4倍して元の立方体の体積から引くだけです。この問題は合格のための必須問題です。
(2) 三角錐ACFH の表面積から,三角錐AIJK の表面積を引いたものが,求める立体の表面積 - △IJK になる事に注意して下さい。三角錐AIJK の表面積と△IJK の面積は,相似を使って求めます。この問題は確実に合格するためには正解出来る事が望ま
しいです。
大問5
(1) 三平方の定理を使って,PA^2 と PB^2 を求めて二次方程式を作れば解けます。この小問は正解して下さい。
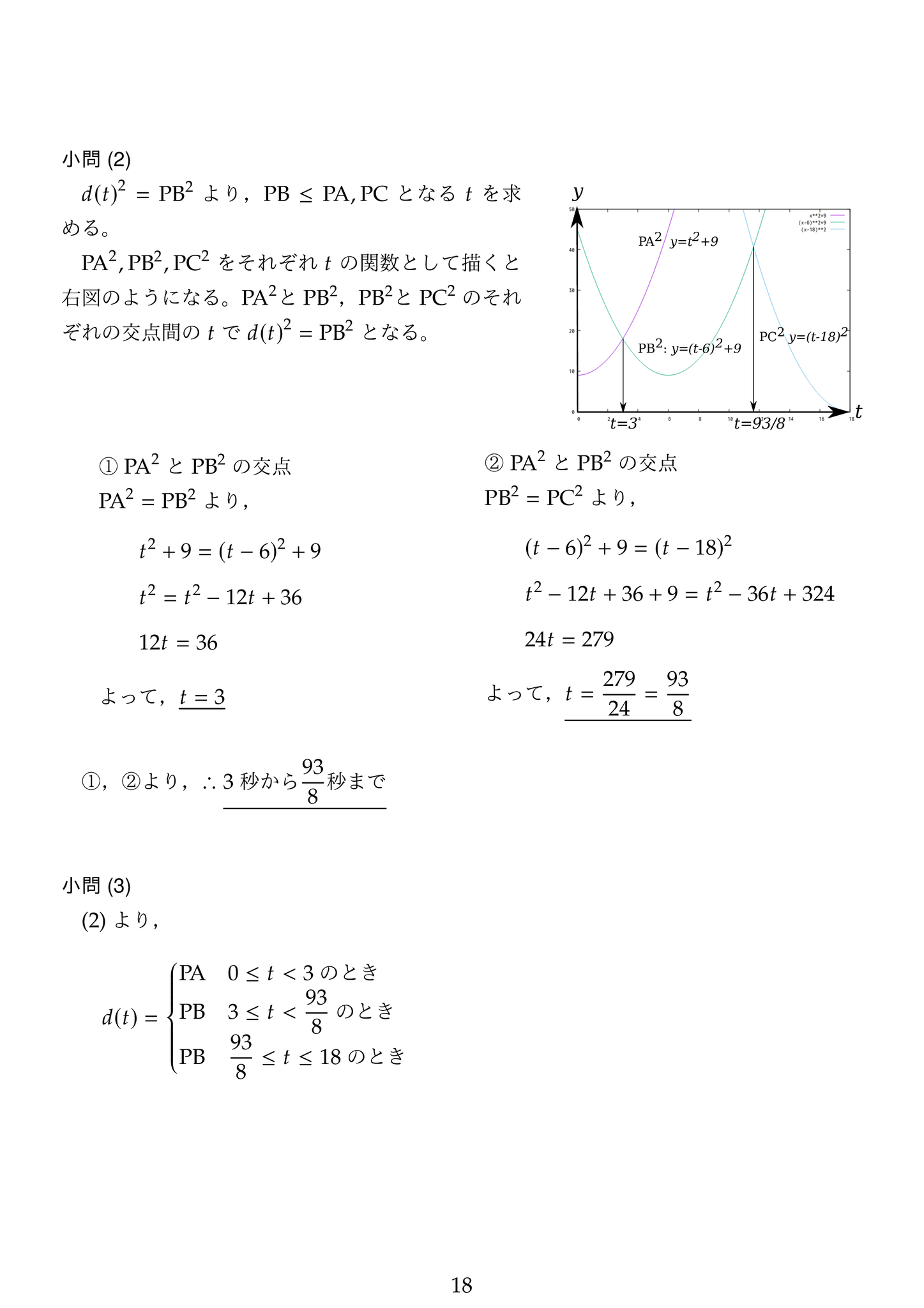
(2) この小問は,高校の数学Ⅰの一般の二次関数のグラフについての知識がないと考えにくいです。
d(t)^2=PB^2 になるのは,PA^2 と PB^2,PB^2 と PC^2,それぞれの交点の間の区間になります。
(3) 前問が解ければ,この小問はそれほど難しくはありません。但し,考え方の筋道を記述させるので,得られた二次方程式の解が t のそれぞれの区間にあるかどうかを明記して下さい。
大問6
(1) 与式を一次関数の形に変形すれば,最初の格子点はすぐに見つかります。残りの格子点は,x が3増加すると y が4減少する事を用いて数えてもいいですが,解答のように高校の数学Aで扱う整数論を使えばきれいな解答が出来ます。
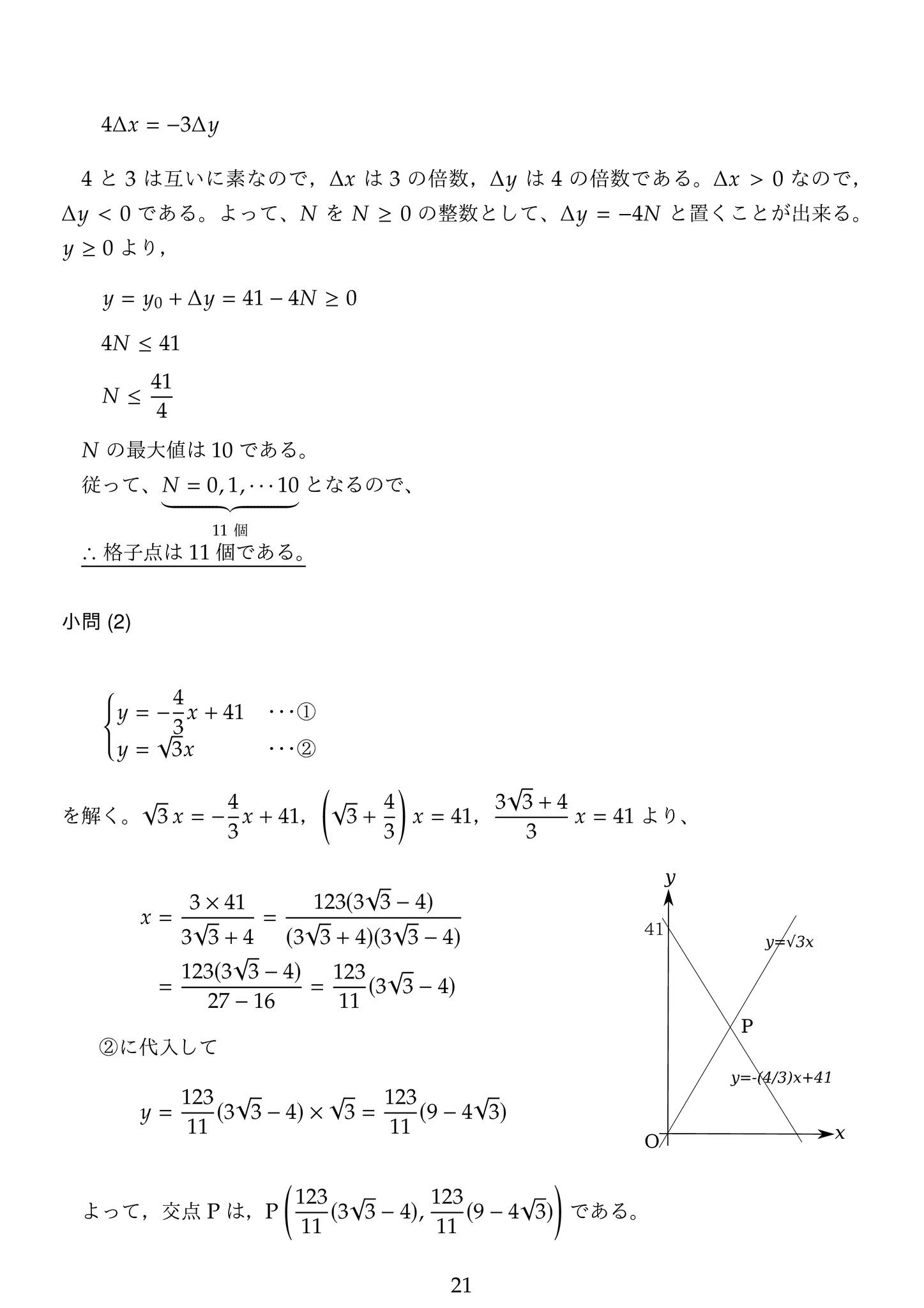
(2) 2直線の交点は等置法(代入法)を用いて求めるだけですが,解が複雑なので正確に計算して下さい。また,高校の数学Ⅰで扱う分母の有理化の計算が必要になります。さらに,この問題は考え方の筋道を記述させるのでここからが問題です。1.7 < √3 < 1.8 を用いると,解答にあるようにPの存在範囲が格子
点を跨いでしまうために隣接する格子点の組を決めることが出来ません。1.7 < √3 < 1.75 は,1.7 < √3 < 1.8 に含まれるのでこの範囲を用いて隣接する格子点の組を求めましたが,√3 が1.7320508 を有効数字3桁で用いてもいいと思います。
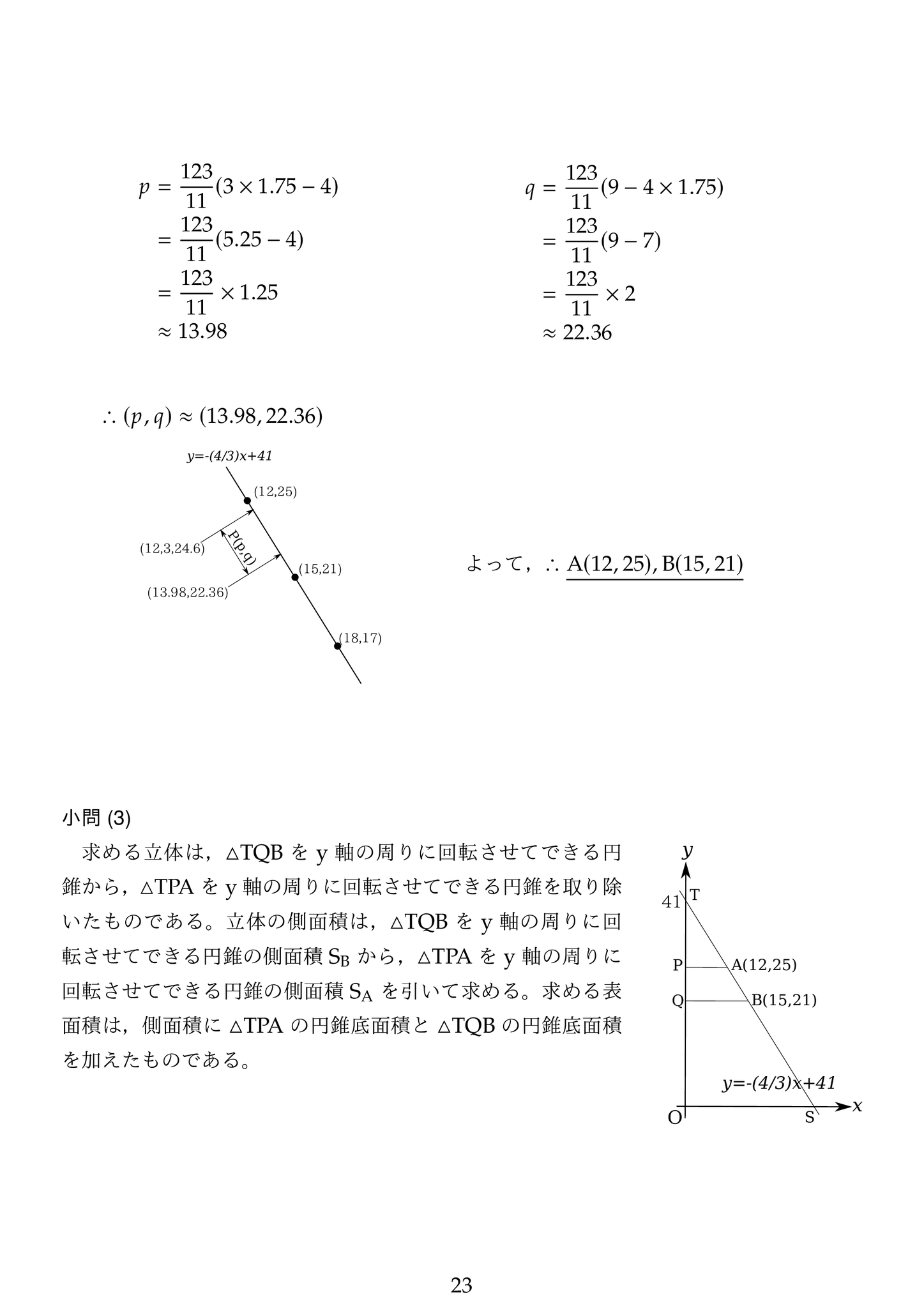
(3) 小問(2)が解ければさほど難しくはありません。求める立体の側面積が大小2つの三角錐の側面積の差になることを用います。なお,計算では解答に示したように素因数分解した形で計算を進めると,間違いが少なく速く計算出来ます。