H30 桃山高校 自然科学科 数学
桃山高校自然科学科の数学問題の詳解です。
概説
今年度の京都府立桃山高等学校 自然科学科の数学の入試問題解説です。できるだけ丁寧な解説を行っています(ページ数が限られている赤本よりも詳しいです)。
桃山の自然科学科の数学は極端に難しい問題はなく,中学3年間の数学を使いこなせれば解ける問題で構成されています。設問総数は,前記共通問題よりも2問少ないですが,大問1の基本問題数が少ないので全体としての難易度は上がります。50分間という限られた時間で完全に解答するのは(私でも)困難ですので取れる問題を確実に得点して,それから得意な問題で点数アップすることが重要です。
大問1と大問2はウォームアップ問題。大問3以降も各小問の(1)は,大問6を除いて基礎問題です。逆に完全な捨て問題の大問がないので,各大問の中で解ける小問を取りこぼしなく得点する必要があります。今年は最後の大問8でも(1)は簡単なボーナス問題でした。桃山自然科学の数学では先ず最初に問題冊子に最後まで目を通して取れる小問を見定めて確実に得点を積み上げる事が必要です。
今年の数学問題でで必ず得点しなければならないのは,大問1(1),(2),大問2(1),(2),大問3(1),大問4(1),(2),大問5(1),(2),問7(1),大問8(1)です。
桃山の自然科学科の入試は,国数理英4教科の独自問題400点と,報告書(内申)100点(3年間の成績135点満点を100/135倍に圧縮),面接25点ですので,ほぼ当日点勝負です。確実な合格のためには当日点の目安として7割以上が必要と思われますので、上記の必須解答問題の得点をスタートラインにして,点数を積み上げて下さい。
今年度の問題で最も正答率が低かったと思われるのは大問6です。特に小問(3)は難しいです。その他,大問4の(3)と記述問題である大問8の(3)も正答率が低かったと思われます。
桃山の自然科学科の数学は7割以上の高得点での勝負になると思われますが,中学3年間の数学を使いこなせれば十分に太刀打ち出来ます。中学数学の基 本事項をしっかり身につけた上で,自由自在に活用出来るように日頃から応用問題に取り組んで下さい。
大問1
ウォームアップ問題です。この2問は絶対に取りこぼさないよう,計算ミスに気をつけて必ず得点して下さい。
(1)は,展開公式を使えるように式を変形して,和と差の積,2乗のの公式を使って下さい。
(2)は,単項式の乗除を正確に計算して,数値を代入すれば OK です。
大問2
大問3
(1)は合計人数と全員の得点総計に関する連立方程式を立てるだけです。総得点=平均点 × 人数 である事を思い出して下さい。
(2)は注意が必要です。この設問における”元の平均点”は前問の5.4 点ではありません。ある元の平均点から得点の修正により,平均点が 0.9 点増加したという設問です(白状すると私も最初勘違いしてしまいました)。
元の配点と修正後の配点に関して,それぞれ平均点の式を作り,
修正後 - 修正前 = 0.9 点という,
問題文をそのまま立式をするのが最も素直な解き方です。
大問4
タイルの塗替えのルールをしっかり頭に入れて考えて下さい。大小2つのサイコロの目の出方は36通りです。
(1)桃色が1枚もなくなるのは,全タイルが塗り替えられて,かつ,2度塗りが起こらない場合です。よって,大小のサイコロの目の和が,タイルの枚数6枚に等しい場合です。
(2)桃色が1枚になるのは,1枚だけ塗替えが起きなかった場合と,1枚だけ2度塗りされた場合です。従って,大小の目の和が5の場合と,大小の目の和が7の場合に分けて数えます。
(3)桃色が他の色よりも多くなる場合を全て考えて下さい。また,サイコロの目の最小値は1なので少なくとも2枚のタイルは塗り替えられます。
桃色が他のどの色よりも多くなる場合は,桃色が6枚,5枚,4枚,3枚の4通りが考えられます。
桃色が6枚と5枚は必ず2度塗りによって起こります。
4枚と3枚は2度塗りが起こった場合と起こらない場合の両方があります。
さらに桃色3枚では必ず残りのタイルが赤と白に別れていなければ,桃色が一番多いことになりません。
以上に気をつけて,全ての場合を数え上げて下さい。
大問5
(1)と(2)はボーナス問題です。必ず正答して下さい。
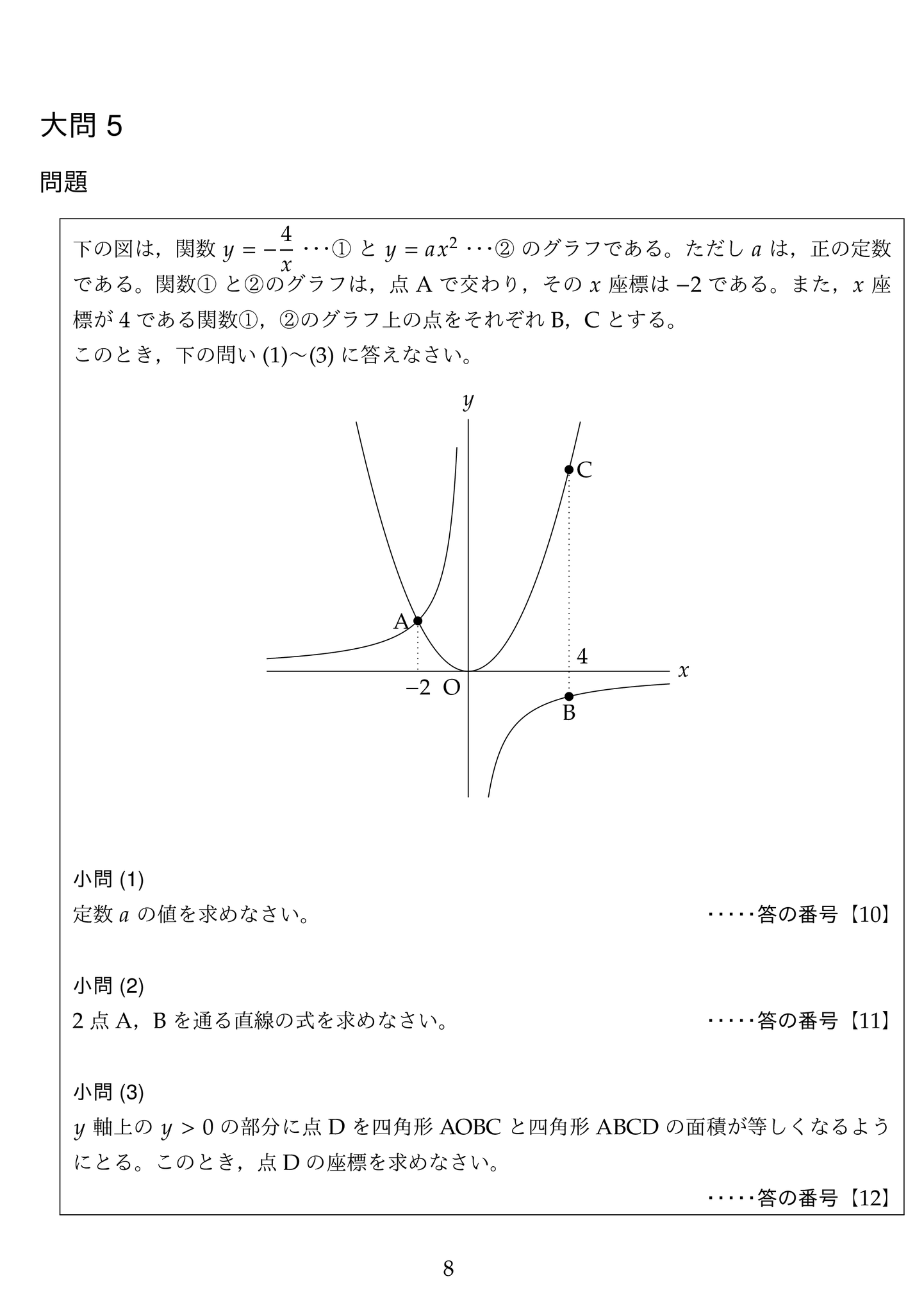
(1)反比例の式が与えられているので,A 点の x 座標を代入して y 座標を求めて,二次関数の式に代入して下さい。
(2)全問と同様に反比例の式に B 点の x 座標を代入して y 座標を求めて,A 点と B 点の座標から直線の式を求めます。解答例のように傾きを計算しても良いですが,y = ax + b としてA,Bの (x,y) 座標を代入して (a,b) の連立方程式を立てて計算することも出来ます。
(3)四角形 AOBC と四角形 ABCD で,△ ABC が重なっていることに気がついて下さい。この三角形を除いた部分の面積が等しければ四角形の面積が等しくなります。
△ AOB と△ ADC が高さの等しい三角形の和であるので,底辺を等しくすれば面積が等しくなります。直線 ACの式を求めると,E点の座標が決まります。FO = ED となるようにD点を決めます。
大問6
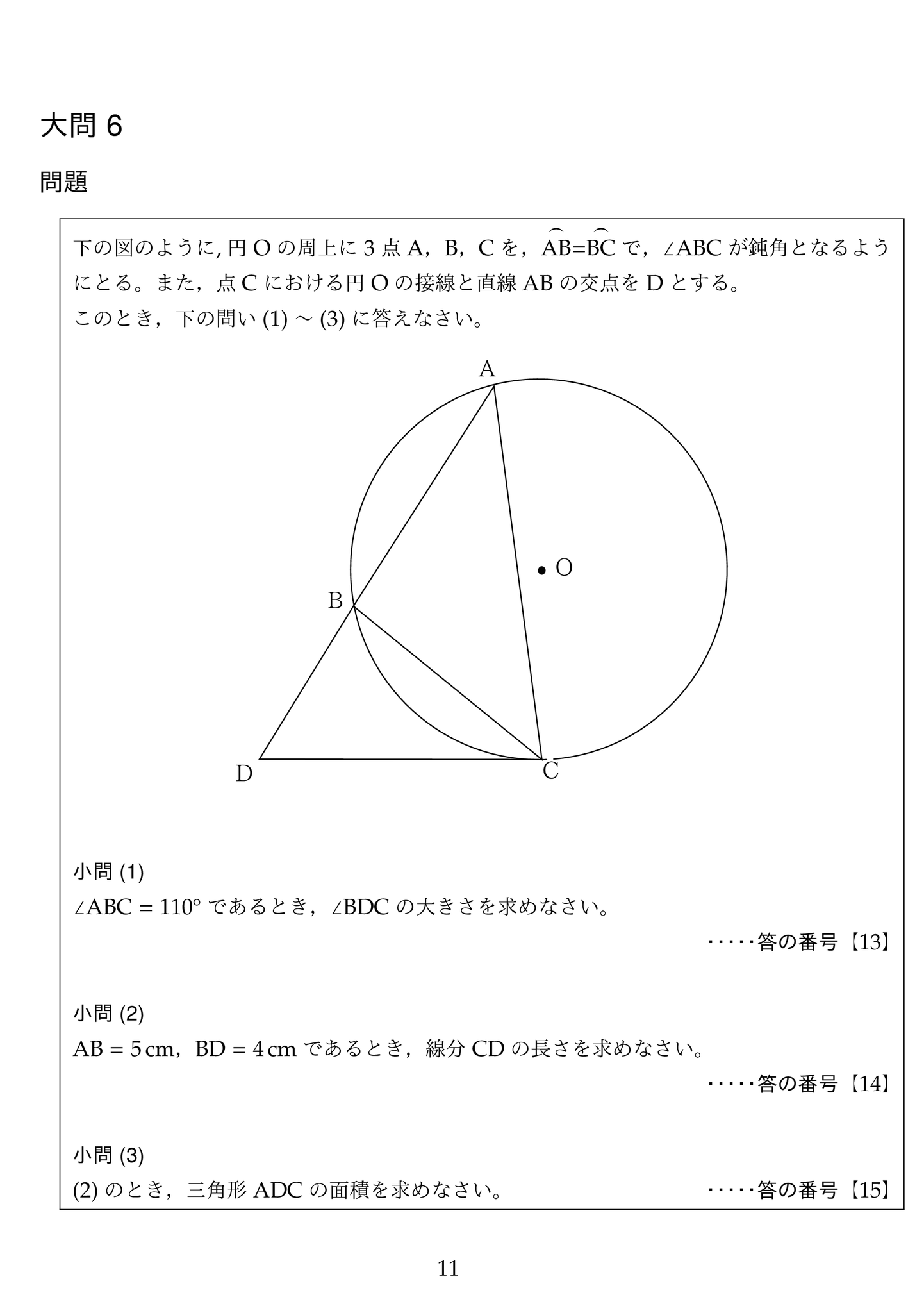
今年の数学で最も難しい問題です。問題文から△ ABC が二等辺三角形であることはすぐに解ると思いますが,接弦定理が理解できているかが正答の決め手になります。また,(1)と(2)は条件が異なる別問題であることに気をつけて下さい。(2)の相似の比例式から二次方程式を作る問題は桃山の自然科学科でよく出題されます。
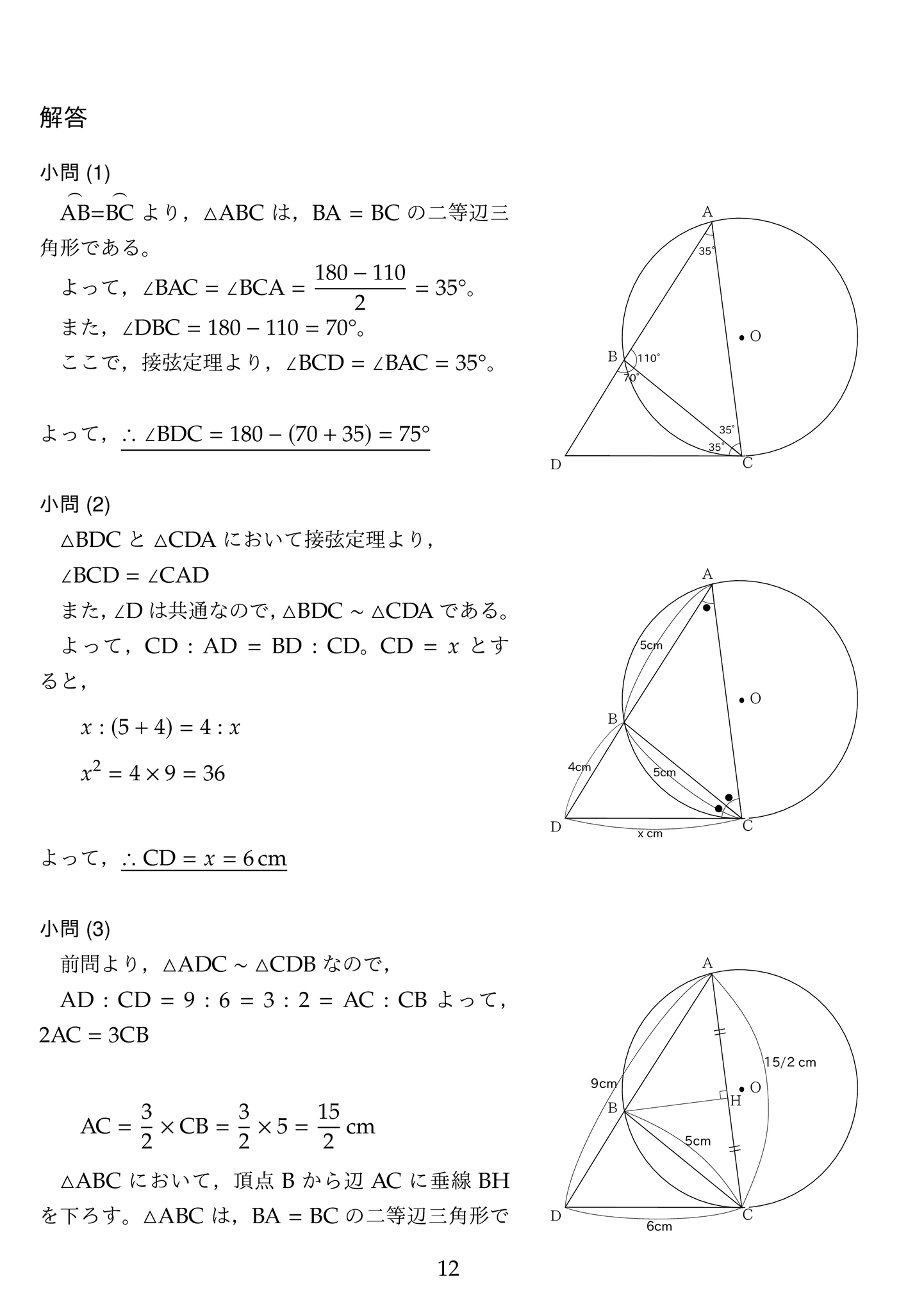
(1)接弦定理より角 BCD と角BAC が等しいことを用いて,△ BCD の内角の和から求めます。
(2)この問題は角 ABC が 110°ではない事に気をつけて下さい。与えられた条件,AB =5 cm,BD =4 cm で考えて下さい(私も最初うっかり角 ABC}=110°として考えてしまいました)。
前問と同じく接弦定理より,角 BCD = 角 CAD が成り立つの
で,△ BDC と △ CDA が相似になります。求める CD を x cm とおいて比例式を作り x の二次方程式を作って求めます。
(3)この小問が今年の最も難しい問題です。前問より△ BDC と △ CDA の相似比が計算できます。その相似比を使って辺BCの長さから辺ACの長さを計算します。
次に △ ABC が二等辺三角形である事を使うと,ABの長さから二等辺三角形の高さが,三平方の定理を用いて計算出来ます。
底辺と高さが決まったので,二等辺三角形△ ABC の面積が求まります。
次に △ BDC と △ CDA の相似比から面積比が決まります。
△ ABC = △ CDA (△ ADC) - △ BDCなので,△ ABC と △ ADC の面積比が求まるので,△ ADC の面積を求めることが出来ます。
大問7
空間図形で三平方の定理が使えるかを問う問題です。
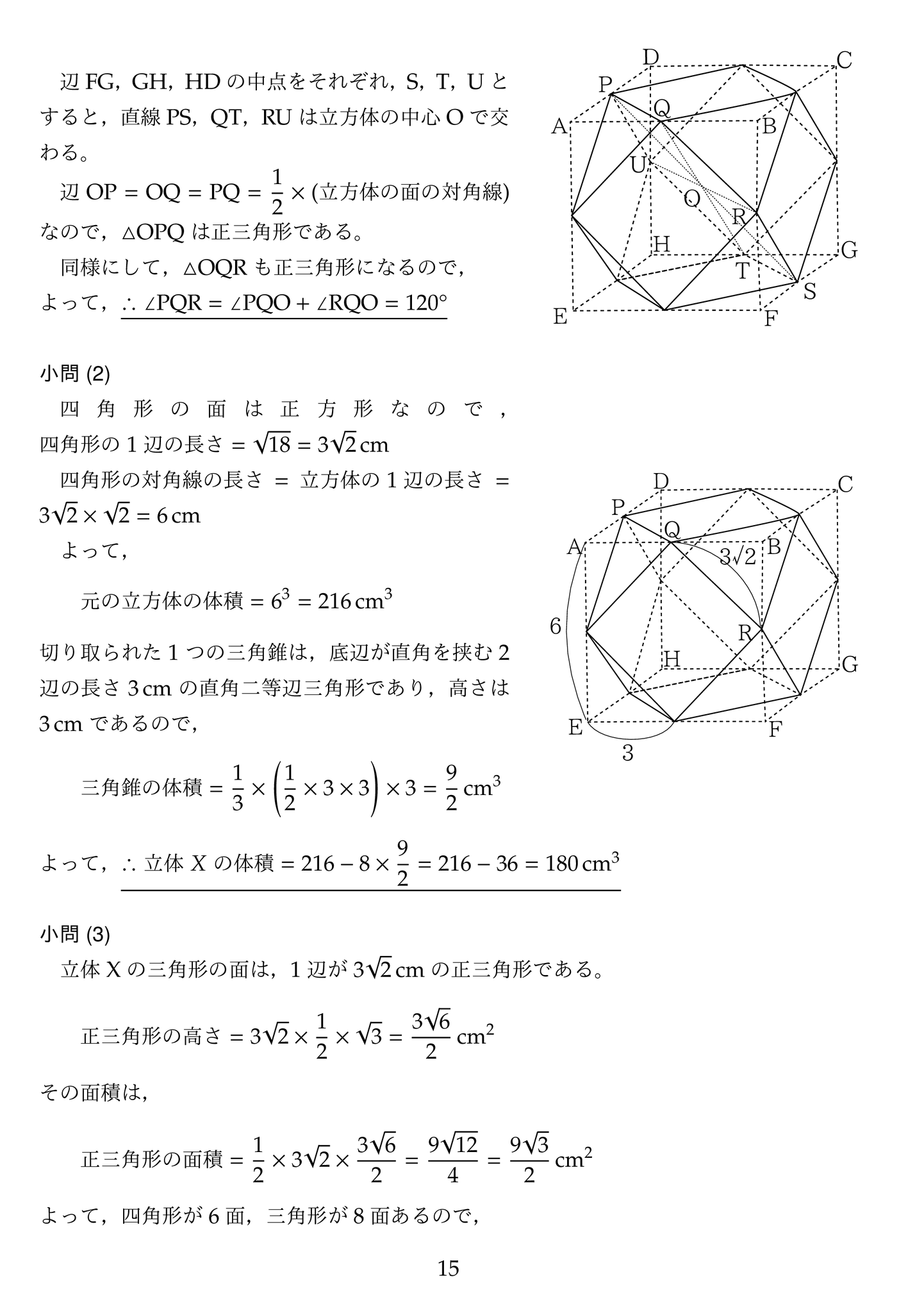
(1)点P,Q,Rを含む平面で切った断面が正六角形になる事に気がつけば正答出来ます。解答例では六角形 PQRSTU が正六角形になる事を示すために △ OPQ が正三角形になる事を用いていますが,問題はそこまで厳密な解答を求めていないので,入試的には直感的に正六角形になることに気づけば大丈夫です。
(2)立体Xの四角の面が正方形になることは直感的に分かると思うので,1辺の長さが面積の平方根で求まり,その四角形の対角線はその √2 倍で,元の立方体の1辺になる事から元の立方体の体積が求まります。
切り落とされた三角錐は,底面が,1辺の長さが立方体の1辺の半分の長さの直角二等辺三角形で高さも同じである事を用いて,切り落とされた三角錐の体積を求めます。
それを8倍して元の立方体の体積から引けば立体Xの体積が求まります。
(3)三角形の面が正三角形であることを用いて,立体 X の1辺の長さから三角形の面積を求めて,四角形の面積6面,三角形の面積8面を足し合わせて表面積を求めます。
大問8
最後の大問で数学オリンピックっぽい問題ですが,(1)はボーナス問題です。正解して下さい。
(1) 2018 ÷ 7 と 2018 ÷ 3 の余りを求めて引き算するだけです。
(2)先ず G(x) に関する二次方程式を解きます。この時,G(x) は自然数を3で割った余りなので取る値が 0, 1, 2 である事に気をつけてください。余りについては高1の数学Aの整数論で正式に学ぶ内容ですが,これまでの経験で分かると思います。2桁の3の倍数の最大値が 99 であるので,3で割って余り1となる2桁の最大数は 99+1-3 です。
(3)難度としてはそれほど高くないですが,記述問題なので論理的な解答を書いて下さい。
G = 0 となるのは3の倍数なので,F(x) + 1 が3の倍数になることが分かります。$F$は7で割った余りなので取る値は0, 1, 2, 3, 4, 5, 6です。従って,F(x) + 1 が取る値は1, 2, 3, 4, 5, 6, 7に限られます。その中で3の倍数は 3, 6 ですで,F(x) =2, 5 となります。100以下の自然数で7で割った余りが 2 になる数の最大値と 5 になる数の最大値をそれぞれ求めて,個数を計算して合計します。