R2年度前期共通問題数学
問題全般の傾向
前期の数学はここ数年難化傾向にあります。R2年度の問題は中位クラスに合格するのに必要な問題の難度は、H30,31年度と同じ程度でしたが、最上位クラスに合格するのに必要な問題の難度が上がりました。幾何の大問3と大問5の最終設問が非常に難しいです。この2問は上位専門学科の独自問題レベルの難度です。規則性の問題は今年は比較的解きやすい問題でした。
大問3の最終設問に関して先日(3月11日)にアップしてから、もっと少ない計算量で解ける別の解法がある事のご指摘を受けましたので、その解法を追加で記載させて頂き、解説書も差し替えました。(3月13日)
この解法を用いると大問3の難易度はかなり下がりますので、今回の最も難しい問題は大問5の(3)です。
問題解説
大問1
(1)〜(3)は基本的な計算問題なので特に問題ありません。
(4)は扇型の面積の公式で、中心角を未知数として方程式を立てて下さい。
(5)は解の分かった連立方程式の係数を求める問題。回を代入して係数の連立方程式を導いて解きます。
(6)は与えられて式を因数分解してから、aの値を代入します。
(7)は二次方程式の解の公式をそのまま適用します。
(8)は関数の概形を考えて、x<0でxが増加する時yも増加する関数を選びます。
(9)は、”少なくとも黒玉が1個残る”→”黒玉が残らない”の余事象として計算して下さい。
大問2
(1)1年生は50人なので中央値は25人目と26人目の冊数の平均値になります。25人目と26人目の入る階級は、6冊以上8冊未満。従って考えられるのは、6冊と6冊、6冊と7冊、7冊と7冊の3つです。
(2)1年生の4冊以上6冊未満の相対度数を求め、3年生の人数にかけると3年生の度数Xが求められます。1年生の8冊以上10冊未満の相対度数を求めると3年生の相対度数Y/40はそれより大きいのでY>12が得られます。3年生の最大の値は16冊なのでZ≧1。先程のXの値を用いてY+Zを計算すると、Y+Z=14。これを満たすYとZは、Y=13, Z=1となります。
大問3
(1)と(2)は簡単な相似の証明とそれを用いた計算ですが、(3)の後半は非常に難しく計算量も多い今回最大の難問です。
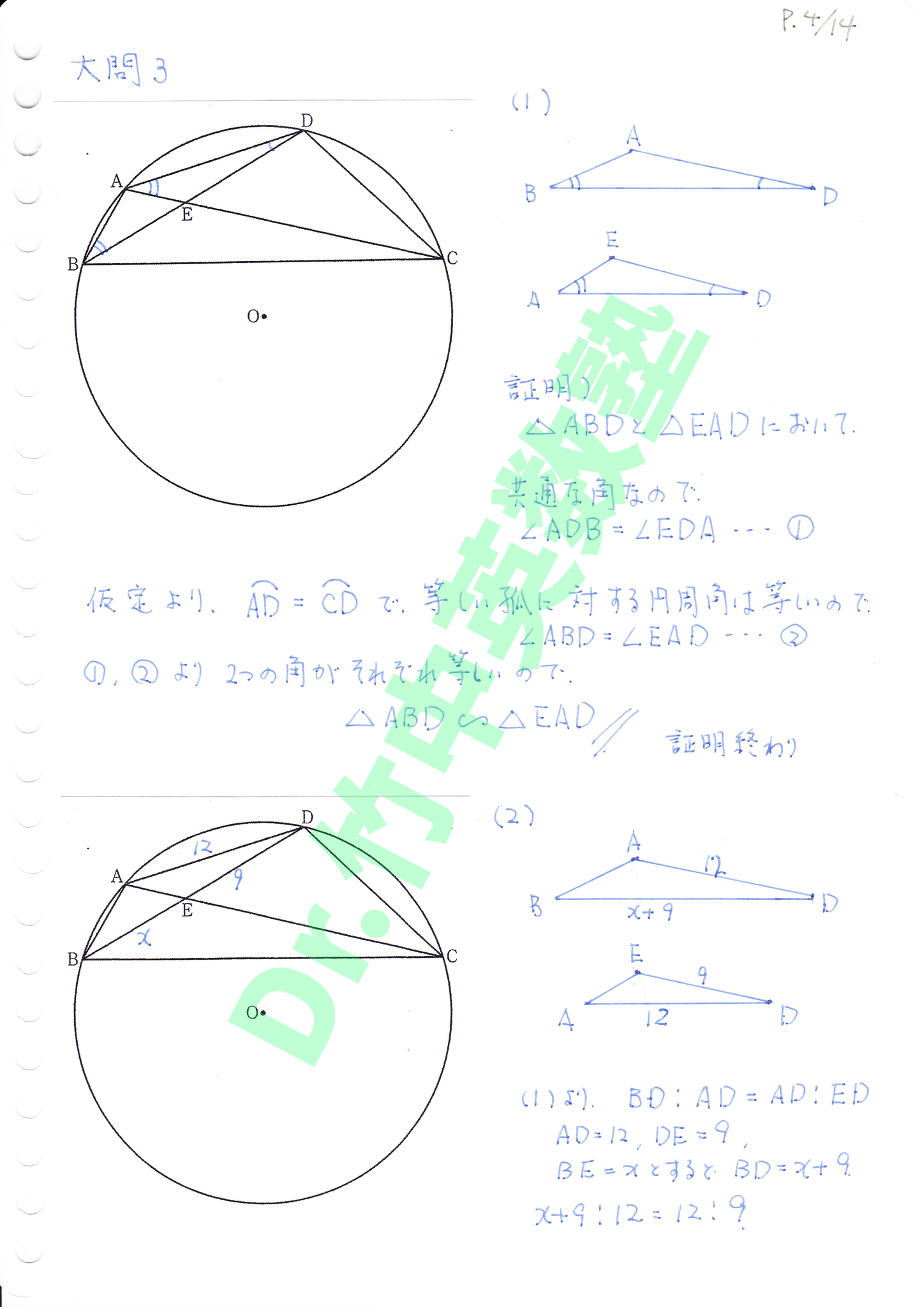
(1)等しい長さの弧に対する円周角が等しいを事を利用して二つの角が等しい相似条件を適用して証明します。
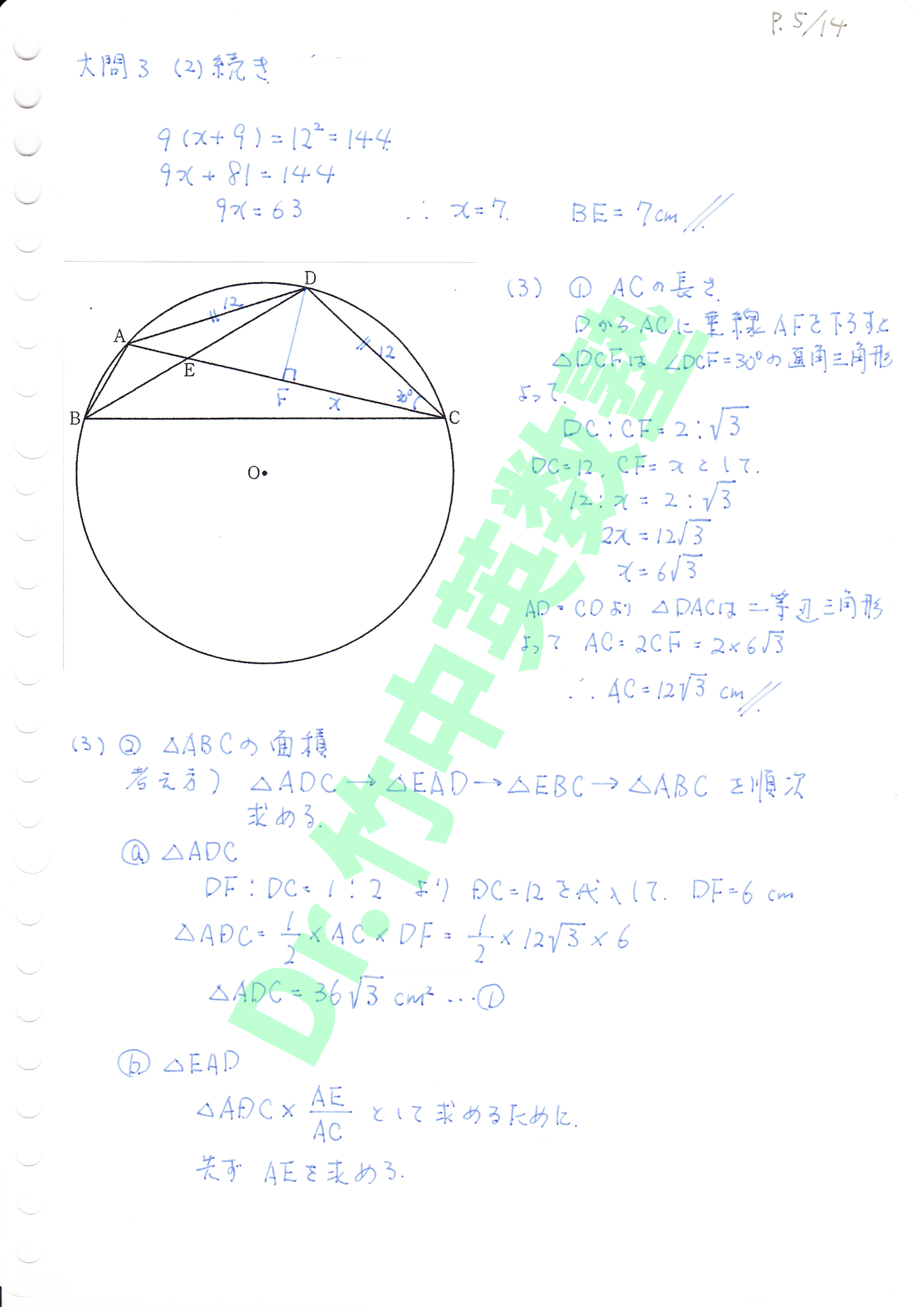
(2) (1)の結果を使います。BE=xとするとBD=x+9、AD=12、ED=9をBD:AD=AD:EDに代入して、x+9:12=12:9という方程式を導いて解きます。
(3)① ACの長さはDからACに垂線DFを下すと△DCF、△DAFが共に30°,60°,90°の直角三角形になるので、DC=12、DC:CF=2:√3を用いてCFを求め、AC=2CFとします。
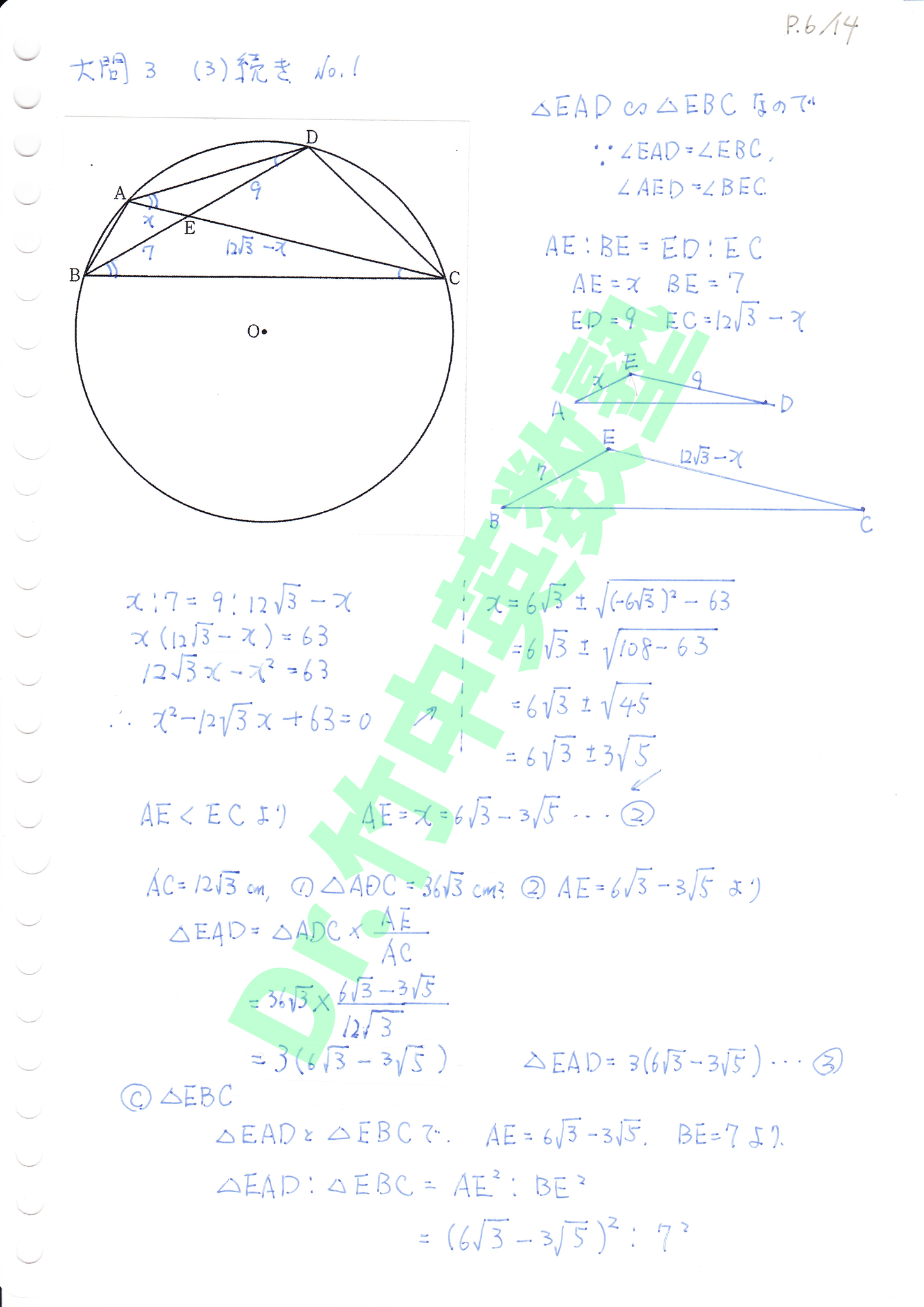
(3)② △ABCは直接底辺と高さを求めるのが困難です。そこで、①の結果からまず△ADCの面積を求めます。次に△EADと△EBCが相似である事を用いてAEを求めて、△ADC×AE/AC=△EADとします。△EADと△EBCの相似比から△EBCの面積が求められます。最後に、△EBC×AC/EC=△ABCとして面積が求まります。非常に計算量が多いので時間内にこの問題を解くのは非常に困難と思われます。
別解を大問6の後に追記しました。↓
大問4
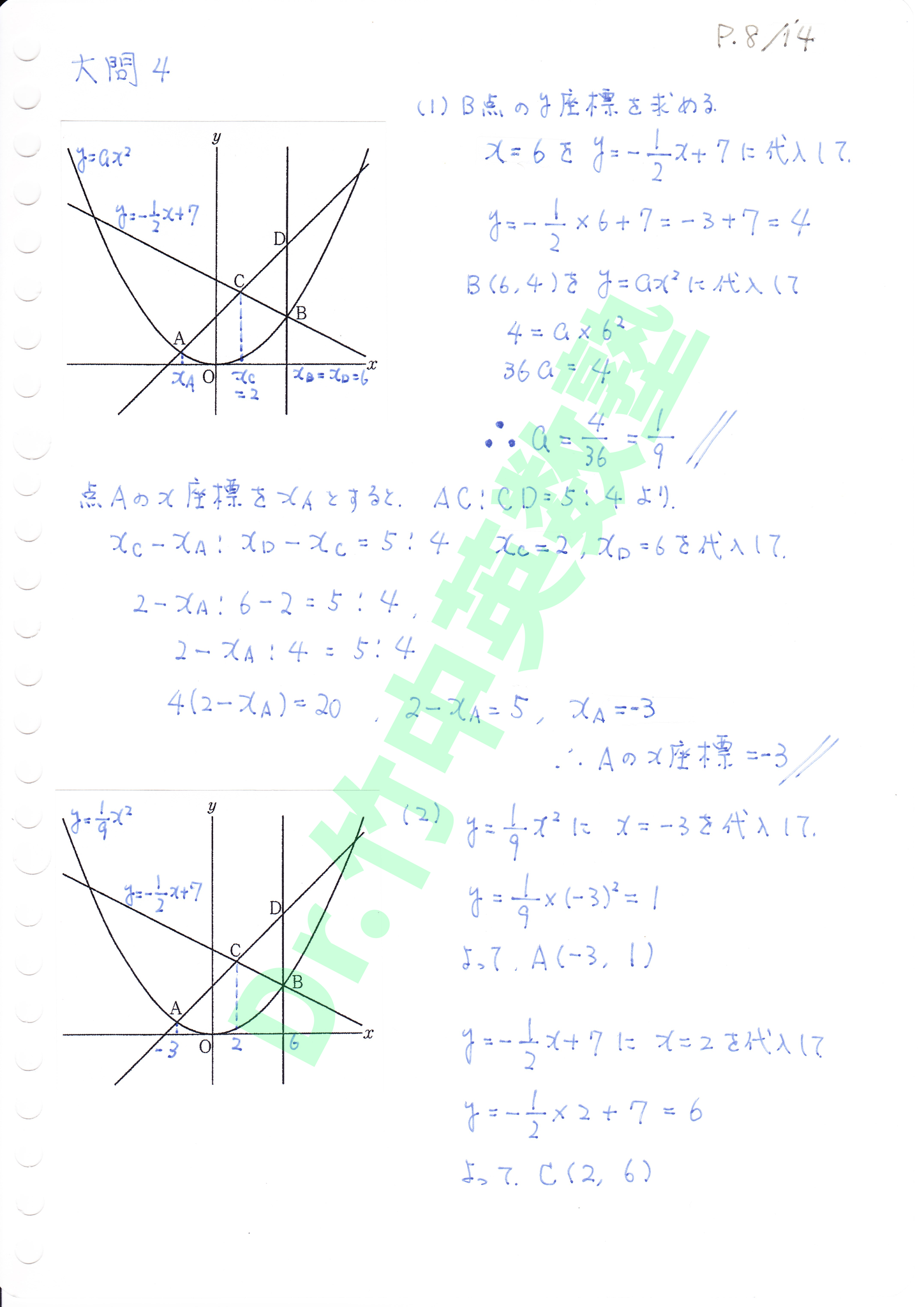
(1)① B点のy座標を直線BCの式にx=6を代入して求め、B点の座標をy=ax^2に代入してaを求めます。
(1)② AC:CD = C点x座標-A点x座標:D点x座標-C点x座標を用いてA点のx座標を求めます。
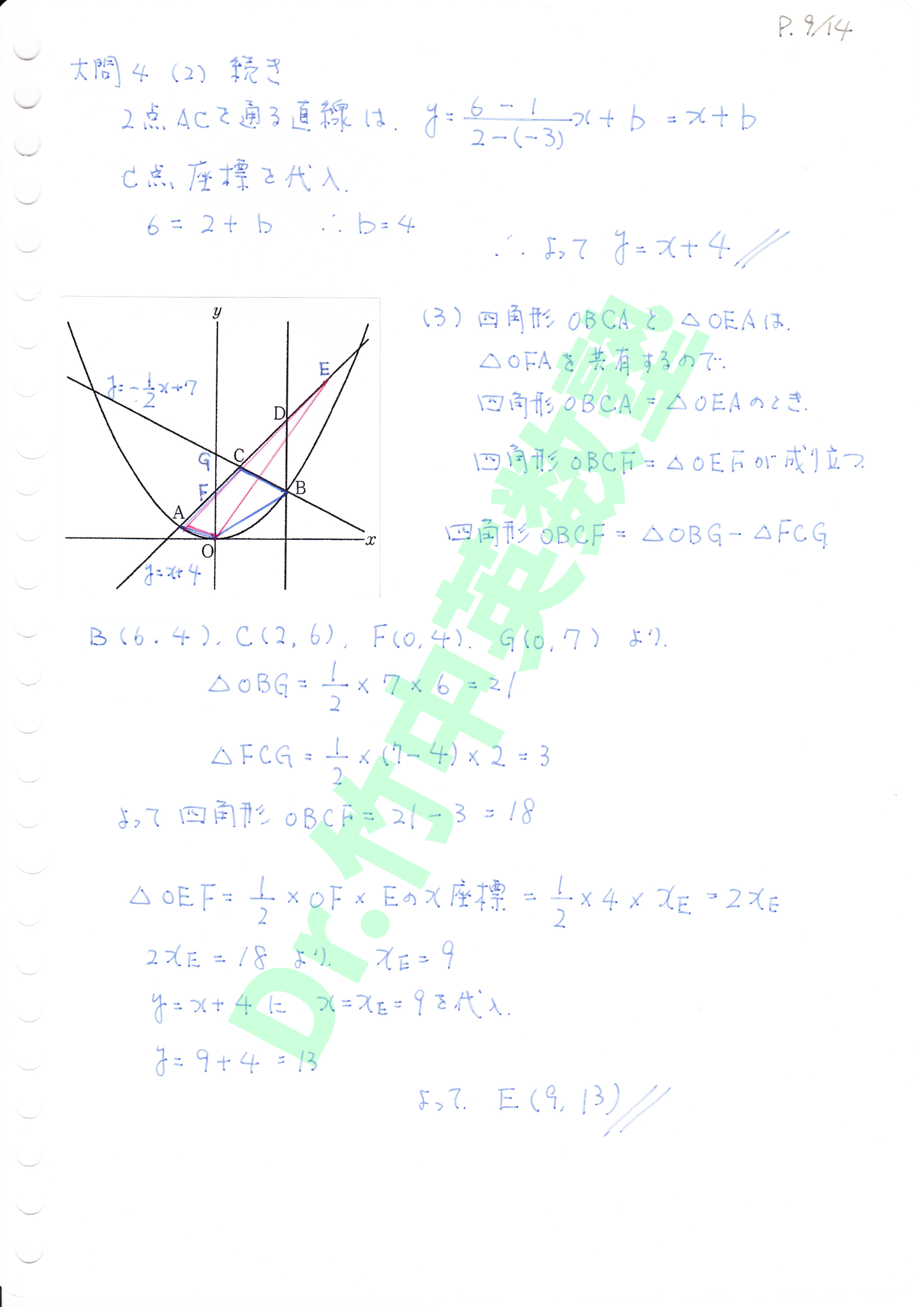
(2)放物線の式にA点x座標を代入してy座標を求め、直線BCの式にC点x座標を代入してy座標を求める。A点とC点の座標から、2点を通る直線として直線ACを求めます。
(3)四角形OBCAと△OEAは△OFAを共有するので、
四角形OBCA=△OEAの時、四角形OBCF=△OEFが成り立ちます。四角形OBCFは四角形OBCF=△OBG-△FCGで求めます。直線BCと直線ACの切片からそれぞれの三角形の底辺OGとFGが求まります。高さはB点とC点のx座標です。△OEFの底辺OFは直線ACの切片です。E点のx座標を未知数として方程式を立てて、求めたx座標を直線ACの式に代入して点Eの座標を求めます。
大問5
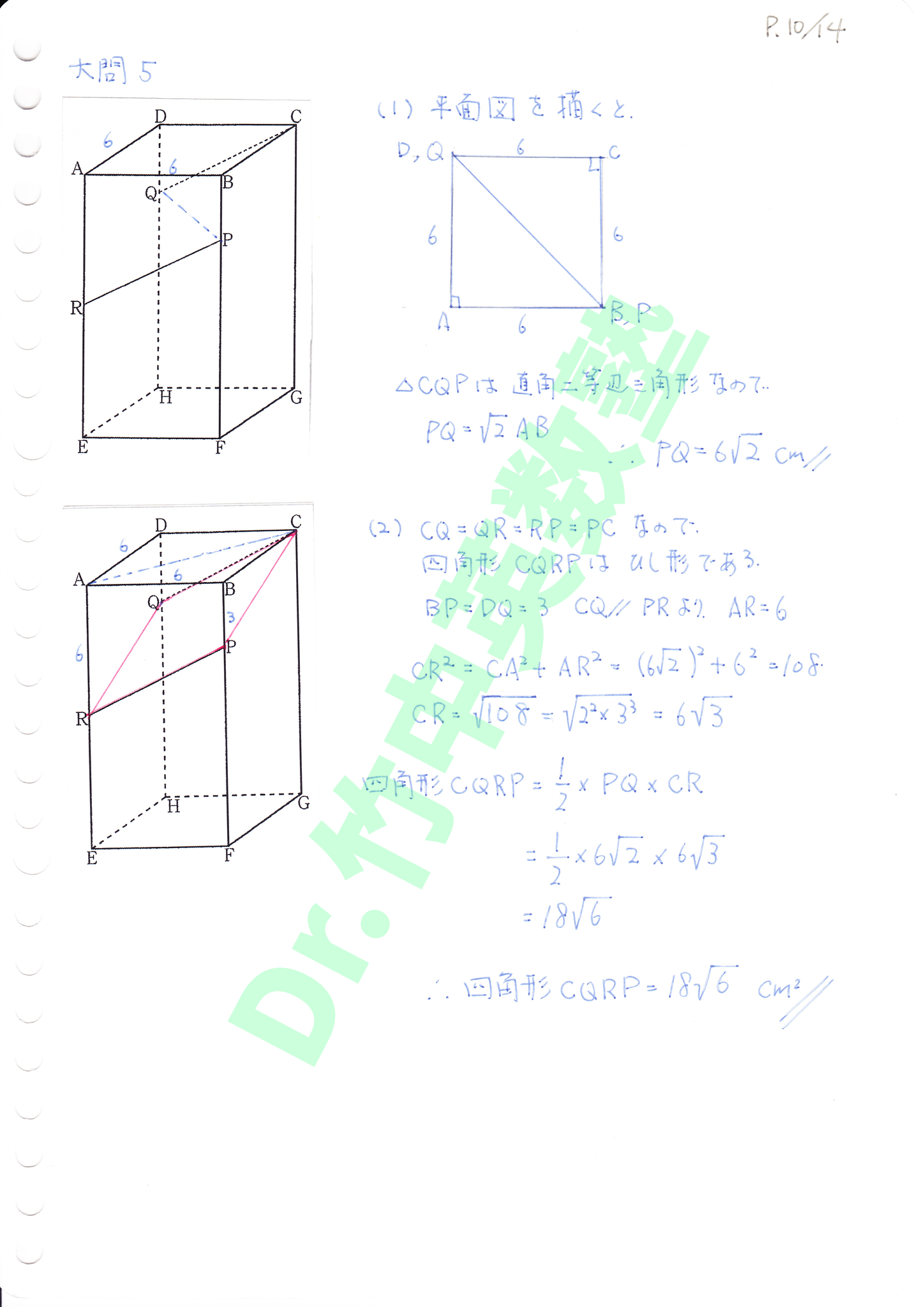
(1)点Pと点Qは同じ高さにあり、四角柱の平面図は正方形になるのでPQ=√2×ACで求めます。
(2)CQ=QR=RP=PCより四角形CQPRはひし形になり、その面積は対角線の積の1/2。CRはAC=6√2, AR=6を用いて三平方の定理で求めます。
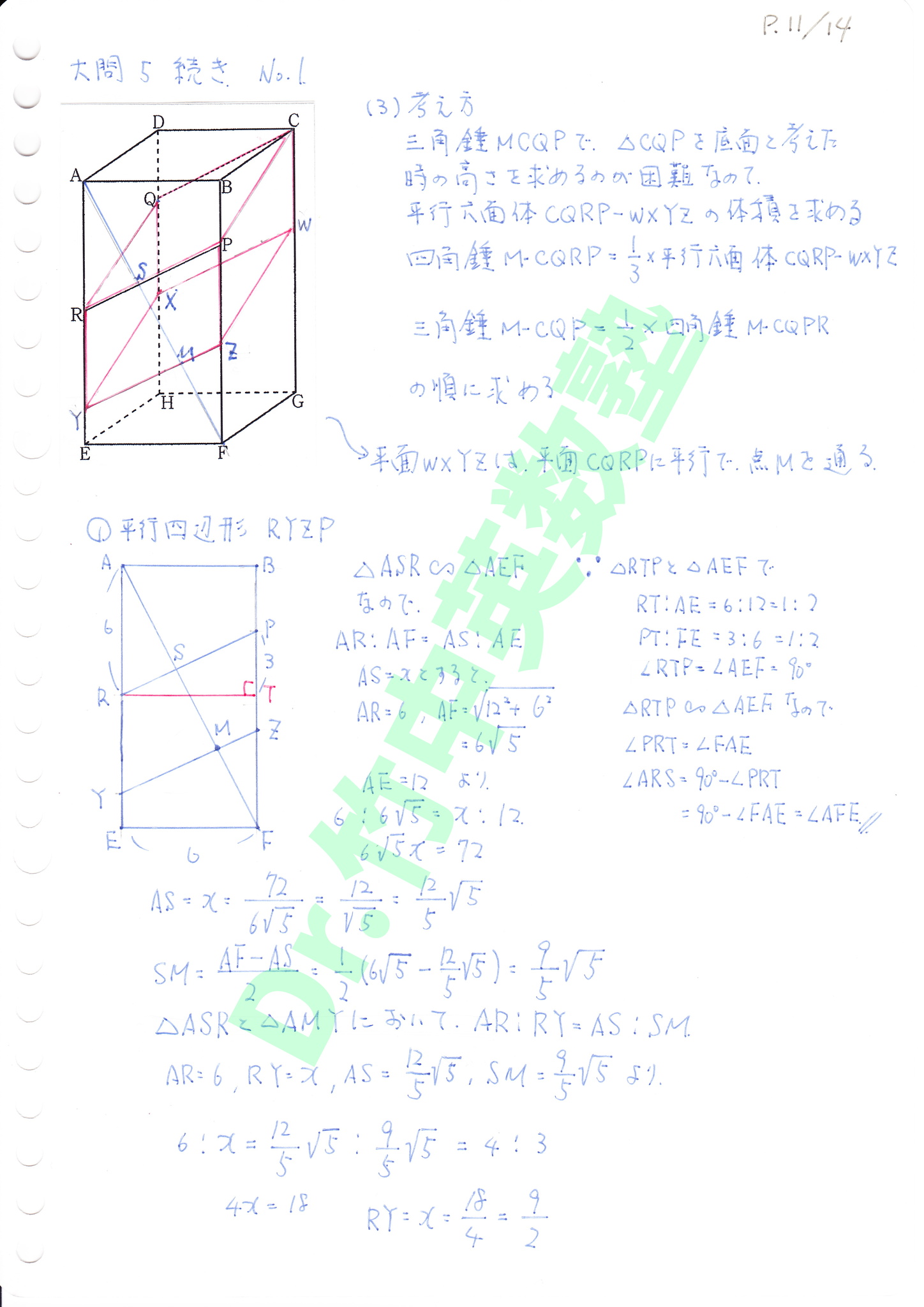
(3)三角錐MCQPで△CQPを底面とした時の高さを求める事ができないので、平行六面体CQRP-WXYZの体積から求めます。三角錐MCQPを含む四角錐M-CQRPは底面をCQRPとすると閉口六面体と同じ高さを持つので、
四角錐M-CQRP=平行六面体CQRP-WXYZ × 1/3
三角錐MCQPの底面は四角錐の半分なので、
三角錐MCQP=四角錐M-CQRP × 1/2
=平行六面体CQRP-WXYZ × 1/6
となります。
この問題も大問3の(3)と同様に難しく計算量も多いです。
実際の計算は解説画像をご覧下さい。
大問6
この問題は、「N (N=1〜9) の箱には、1〜nまでにあるNの倍数の個数の玉が入る」と読み替えれば簡単に解けます。
(1) N=6の箱で初めて3個入るのは、n=6×3=18回目(ア)、初めて4個入るのは、n=6×4=24回目(イ)となります。
(2) a回目で3の箱に赤玉が初めてb個より、
a=3b…①、
そこから85回目の操作で8の箱の赤玉が初めてb個より、a+85=8b…②
①と②を連立方程式として解いてa, bを求めます。
(3)n回目で4の箱の赤玉の個数と9の箱の黄玉の個数が等しくなったと考えます。
267回目までの4の箱の赤玉の個数、9の箱の赤玉の個数を求めます。n回目で9の黄玉の個数が4の赤玉の個数に等しくなるから、n回目での9の箱の玉の総数(赤と黄の合計)が求まります。この合計数×9=nです。
nの値から4の箱の玉の総数が求まり、総数-赤玉の個数=黄玉の個数となります。
実際の計算は説明画像をご覧下さい。
大問3 (3) の別解法
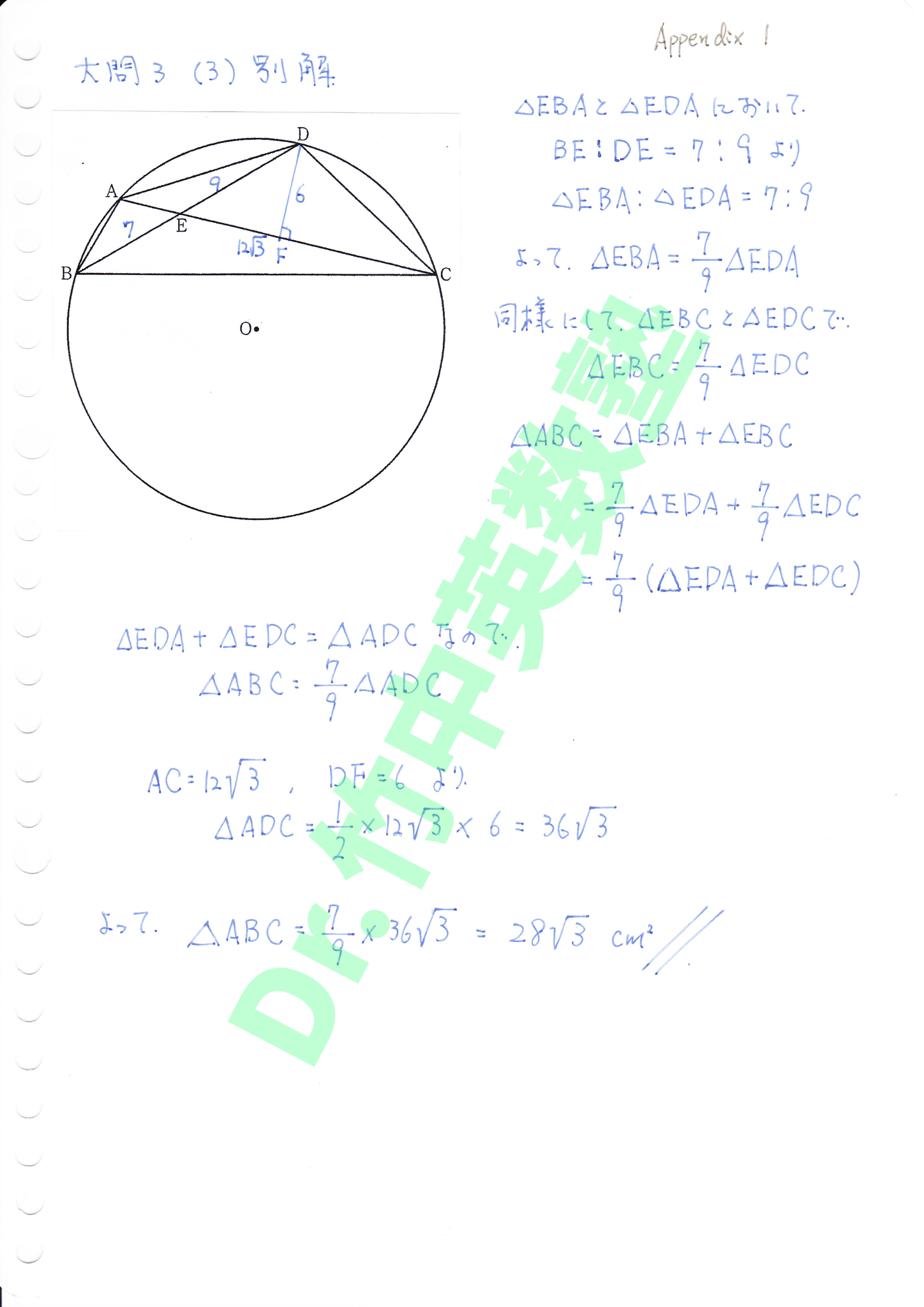
(2)の結果、BE:DE=7:9 を用いると、△EBAと△EDAにおいて
△EBA : △EDA = 7:9、
よって、△EBA=△EDA×7/9
同様にして、△EBC と△EDCにおいて
△EBC=△EDC×7/9
△ABC=△EBA+△EBC=(△EDA+△EDC)×7/9
△EDA+△EDC=△ADCなので、
△ABC=△ADC×7/9
△ADC=12√3×6/2=36√3
よって、
△ABC=36√3×7/9=28√3
この解法の方が計算量が少なく、容易に求められます。出題者が想定していたのは、こちらの解法だと思われます。