R5年前期共通問題数学

(1)〜(4)は基本的な計算問題ですが、ほぼ全員が得点できる問題なので、不注意なミスで間違えない事です。

(5)はy=ax^2の変化の割合を求める公式を覚えている事が重要です。

(6)と(7)も簡単な計算問題ですので不注意ミスをしない事。

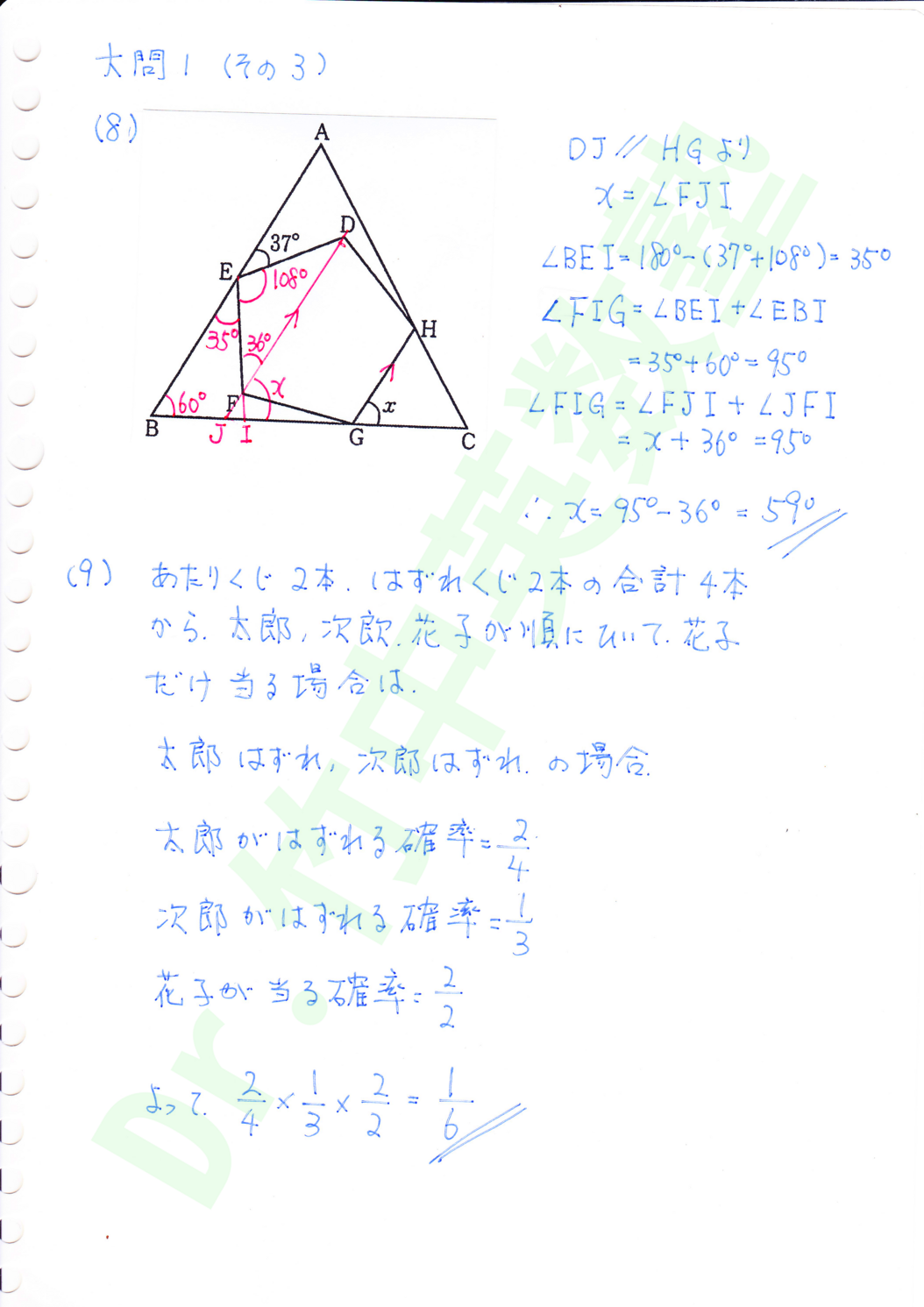
(8)は昨年までよりも難しくなりました。平行線の間に正五角形がある問題は過去に有りましたが、正三角形内部は初めてです。求める角を作るGHに平行な対角線FDを考えつくかがポイントです。

(9)は、太郎、次郎、花子が順にくじを引いて花子だけ当たるという問題文から、太郎と次郎がともに外れると読み替える事がポイントです。

(1)生徒9人が拾ったペットボトルの合計からaとbの二元一次方程式はすぐに導けますが、連立する式がありません。生徒の拾った本数が全て異なることから、当てはまるa, bを求めます。

(2)四分位数の問題です。四分位範囲を理解している事がポイントです。第1四分位数を仮定して、与えられた四分位範囲から第3四分位数を求めた時に、それが第3四分位数になるかどうかを試して下さい。

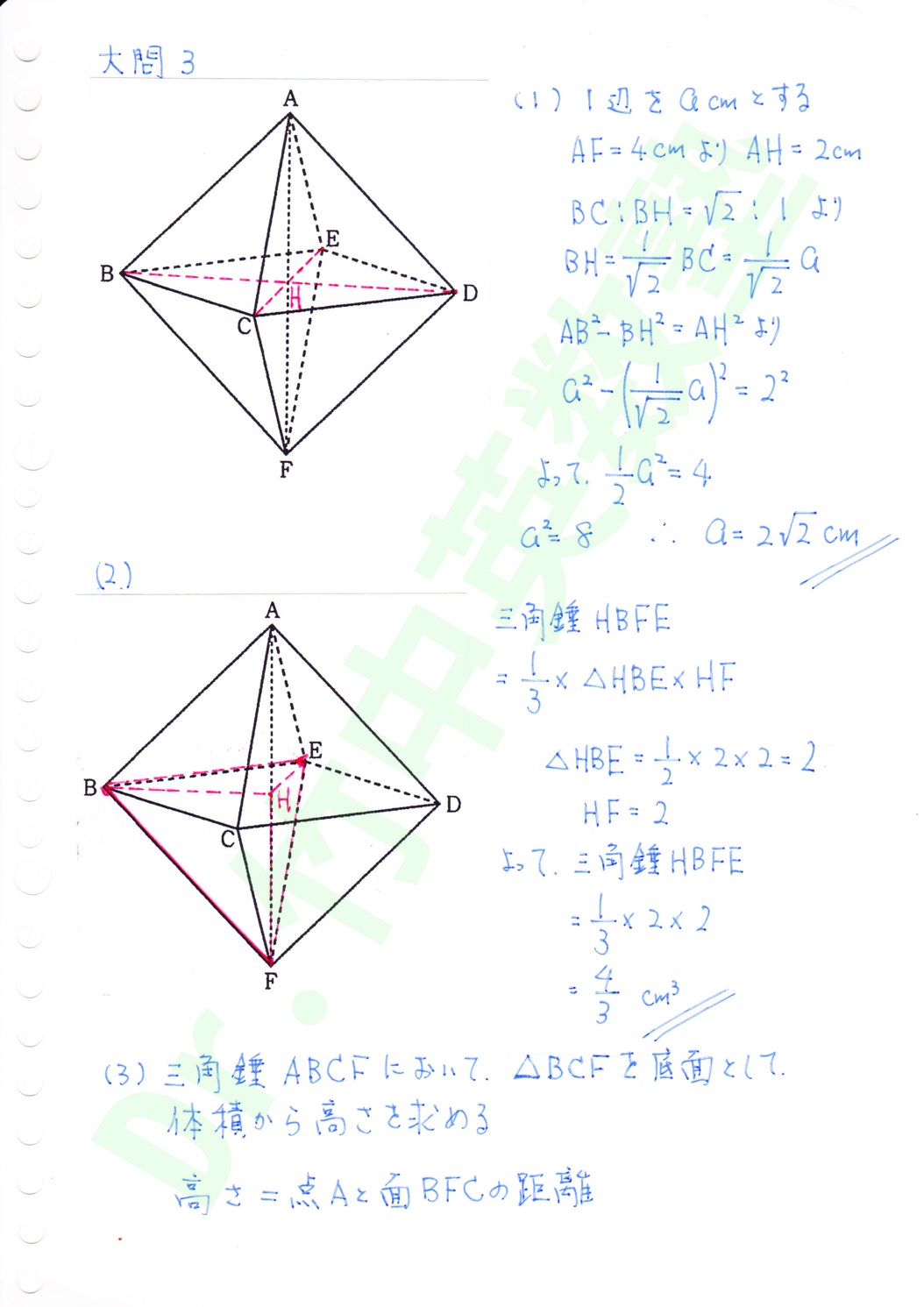
(1)昨年までの問題ならば、1辺の長さから四角錐の高さを求める出題でしたが、本年は高さから1辺の長さを求める問題で、戸惑った受験生がいたと思います。1辺の長さをaとして二次方程式を立てて1辺の長さを求めます。

(2) (1)の結果を使います。与えられたAFからHFを求めて、三角錐HBFEの高さとします。△HBEを底面として(1)の結果から底面積を求めて三角錐HBFEの体積を求めます。

(3)三角BCFを底面と考えた時に三角錐ABCFの高さが頂点Aと面BCFの距離になります。三角錐ABCFの体積は(2)で求めた三角錐HBFEの2倍です。△BCFの面積は正三角形の1辺と高さが、2:√3になる事を使って求めて下さい。後は求める距離をdとして、三角錐ABCF=△BCF×d/3をdについて解いて下さい。

(1)前半の反比例の比例係数を求める問題は容易ですが、後半の三角形の面積を求める問題は等積変形が必要です。最初の設問から等積変形が必要になるのは中位レベルの問題の難化の特徴です。直線ABの式を求めて点Cを直線ABに平行に移動してy軸上に移してDEを底辺とする三角形に変形して面積を求めます。

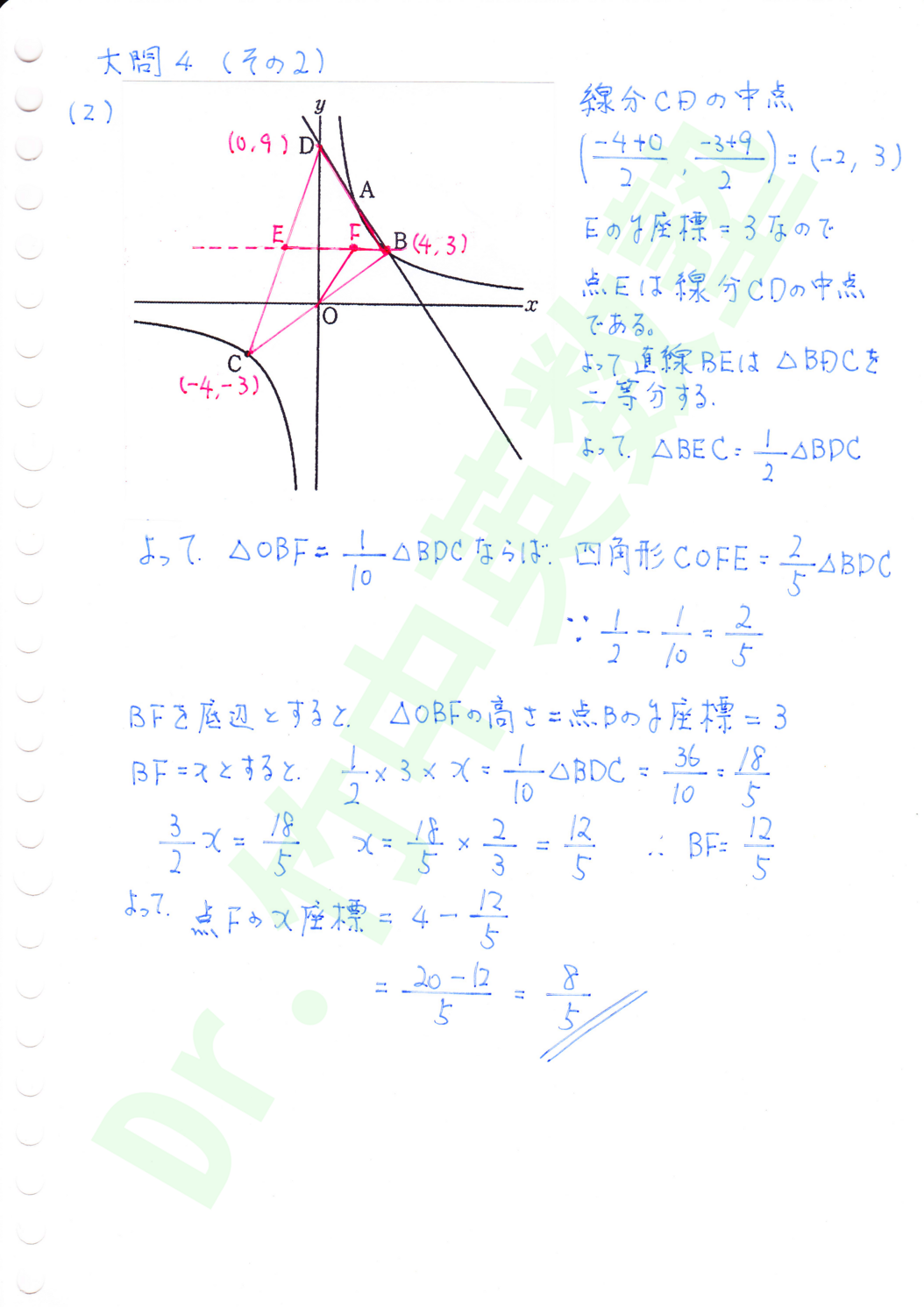
(2)与えられた面積に分割する時の定石は等積変形ですが、それが使えない問題です。直線BEが△BDCを二等分する事に気が付けるかがポイントです。△BEC=△BDC/2より、△OBFが△BDC／10になれば、四角形COFE=△BDC×2/5になります。△OBFでBF=xを底辺、高さを3として面積が△BDC／10になるようにxを求めます。

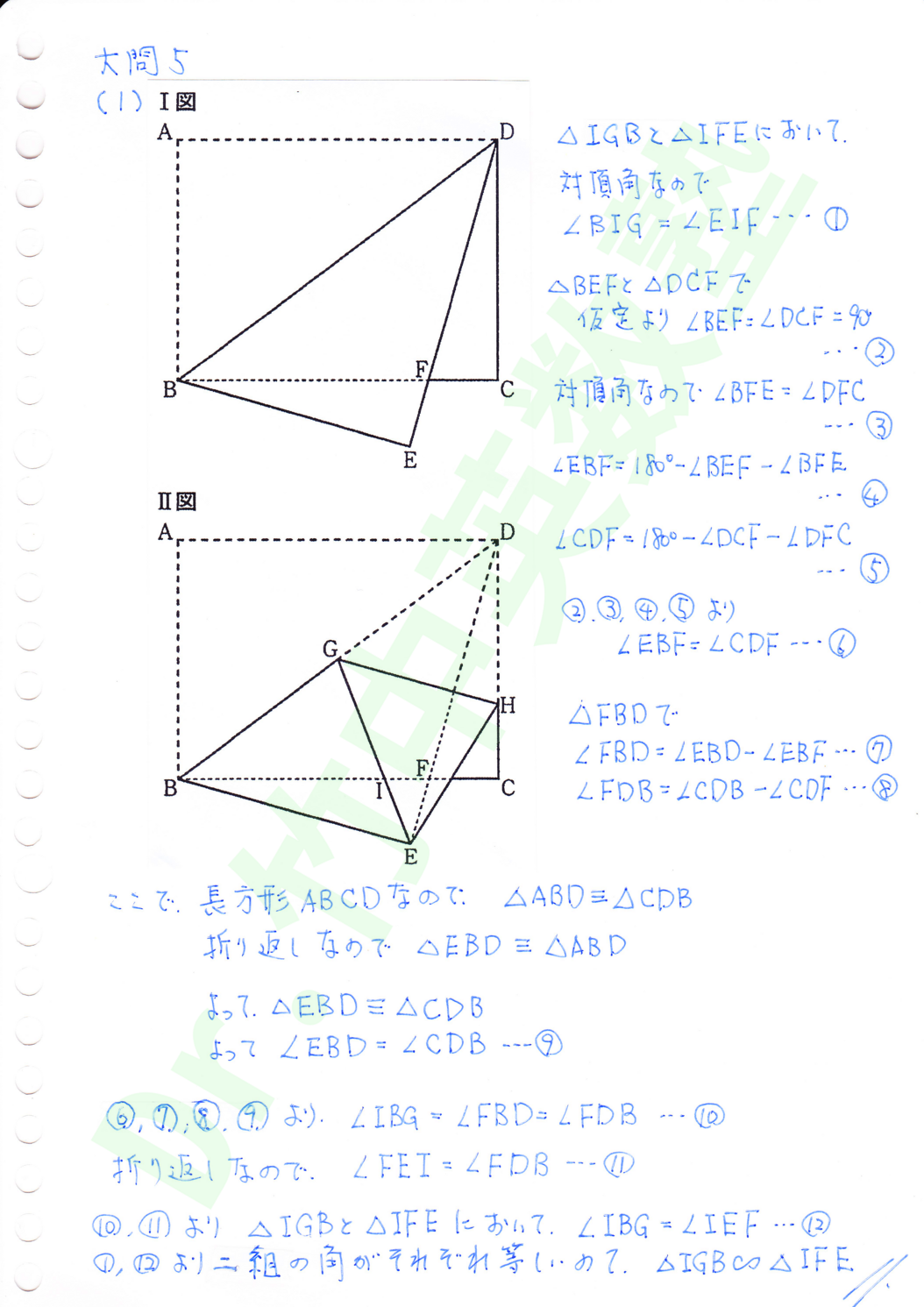
(1)証明の記述問題ですが、昨年までよりずいぶん難しくなりました。折り返した図形では等しい角や辺が増えるからです。しかも2回折り返されています。証明を載せますが正直な所、冗長であまり良い証明ではありません。お手本の証明は解答をご参照ください。冗長な証明になった原因はⅡ図で線が入り組んでいるので、うっかり平行線の錯覚を見落としたのが原因です。

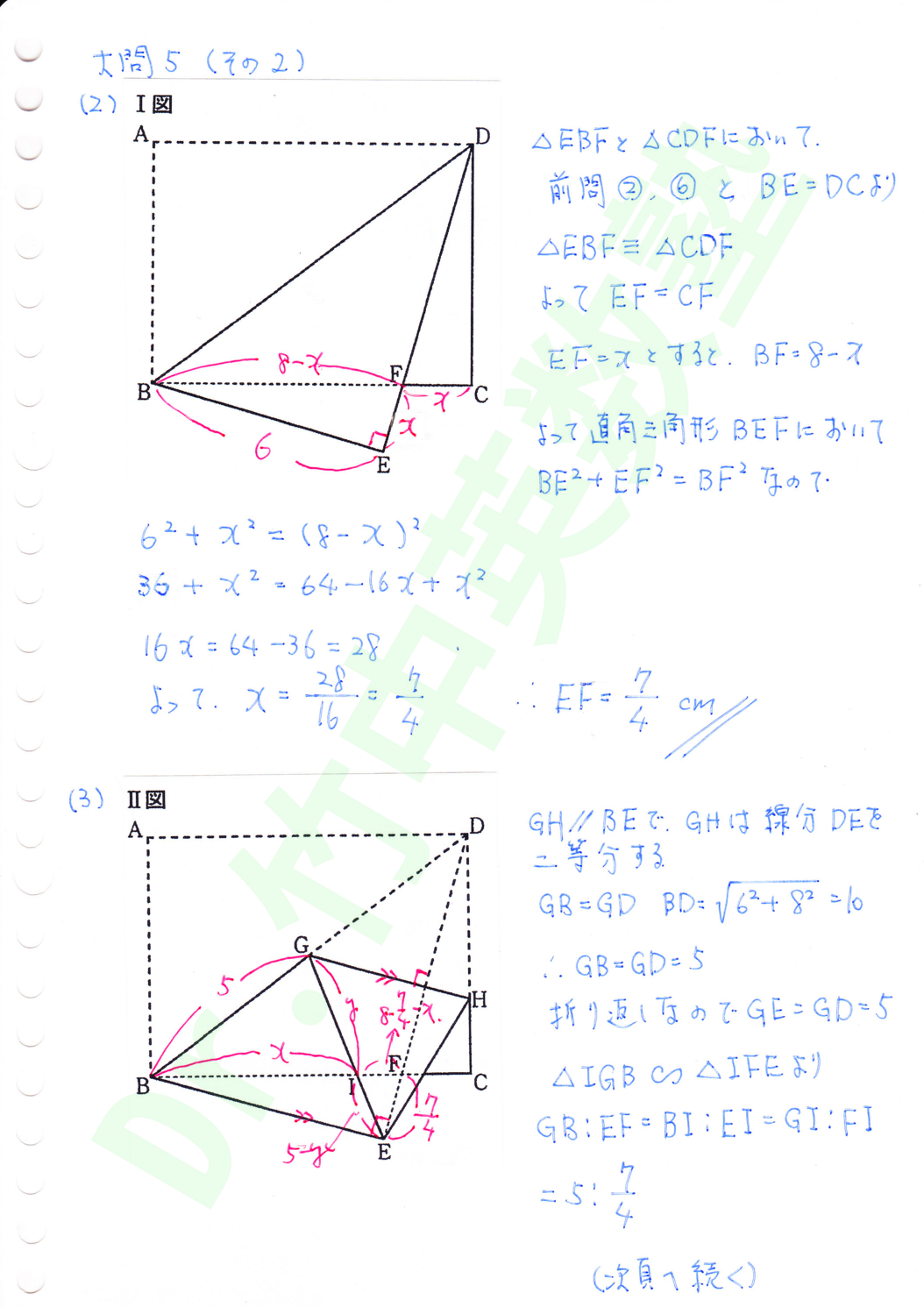
(2)Ⅰ図を見ると解きやすいです。△FBDが二等辺三角形で、DE=BCであることから、EF=xとおくと、FC=x、BF=8-x、BE=6、を使って直角三角形BEFについて三平方の定理で方程式を立てて求めます。

(3)今回の最も難しい問題です。辺の比に関する方程式を立てる問題は、二次方程式になるものも含めて、過去にもあった筈ですが、今回は連立方程式が必要になります。

(1)の△IGB∽△IFE、(2)の結果、及び、△GBEがGB=GE=5の二等辺三角形である事を使います。BI=x, EI=yとして、BI:IE=GI:IE=5:4/7よりx, yの連立方程式を導いて、xを求めます。

規則性の問題ですが、それほど難しくありません。規則性の問題が簡単になったのは昨年の中期選抜からの傾向の様です。

(1)1周目は右と上が1、左と下が2です。1周外側に行くに連れてそれぞれ2ずつ増えるので、右と上は1, 3, 5, 7, …、左と下は2, 4, 6, 8, …となり、表のような本数になります。

(2)20が入力された時の左矢印の合計は、2+4+ … +40です。これは高校の数Bで履修する等差数列の和の問題ですが、最初と最後を足して個数をかけて2で割ります。

(3)上＋左＋下ー右＝左＋下になります。入力した数をnとすると、1+2+3+ … +n=1540となります。

左辺の合計は最初と最後の和に個数をかけて2で割るので、

n(n+1)/2=1540

この二次方程式を解いて、n=55を求めます。